5 Numrical Analysis

Errors

Assume that r is the root of function $f(x)=0$.

• Forward Error: $|r-x_a|$
• Backward Error: $f(x_a)$
• $\text{error magnification factor} = \frac{\text{relative forward error}}{\text{relative backward error}}$

Basic Arithmetic

Evaluating a polynomial

Direct form:O($n^2$)

$P(x)=a_0+a_1x+a_2x^2+...+a_nx^n$

Horner's method:O(n)

$P(x)=a_0+x(a_1+x(a_2+x*(...(a_{n-1}+a_nx)))$

Example:求二进制幂O(n)->O($\log n$)

$a^n=a^{p(2)}$$=a^{b_m2^m+...+b_i2^i+b_0}$

$a^{2p+b_i}=a^{2p}*a$ or $a^{2p}$

Multiplication

Calculate $x=yz$

we could devide y and z into 2 parts of $\frac n2$ bits

y	a	b
z	c	d

Then follow the 4 equations, we only need 2 $\frac n2$ bits muliplications to calculate v and w

$$\begin{cases} u = (a+b)(c+d) \\ v = ac \\ w = bd \\ x= v2^n + (u - v - w)2^{\frac n2} + w \end{cases}$$

For u, we could proof that we just need 1 $\frac n2$ bits muliplication + some addition and shift

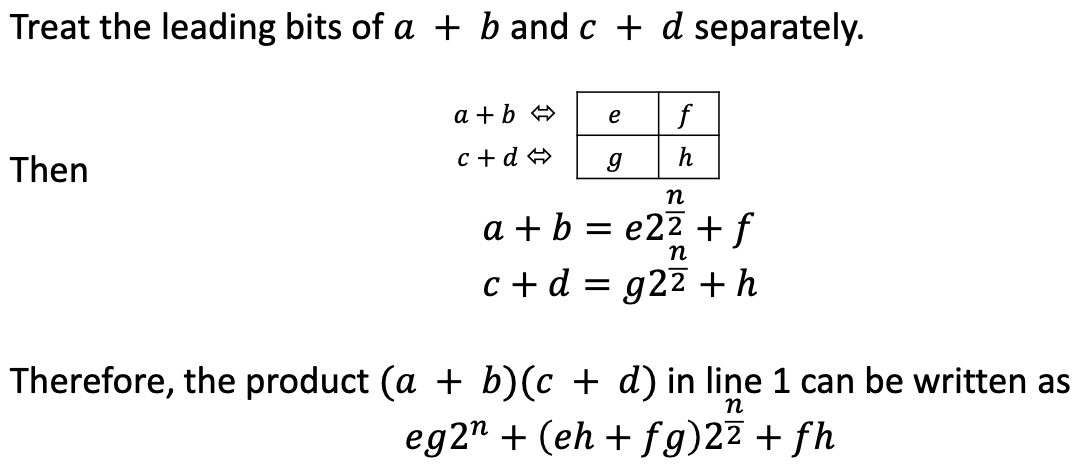
$T(n) = 3T(n/2) + ln \Rightarrow T(n) = O(n^{\log_2^3})$

Solving Equations

Newton's Method

$x_0=initial\ guess$

$x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)}$

Convex Optimization

Convex combination: $(x,y)\rightarrow\{\alpha x + \beta y|\alpha + \beta =1, \alpha,\beta \geq 0\}$

Convex set S: $(x1, . . . , xk) \in S$, then convex combination of the points x1, . . . , xk should $\in$ S.

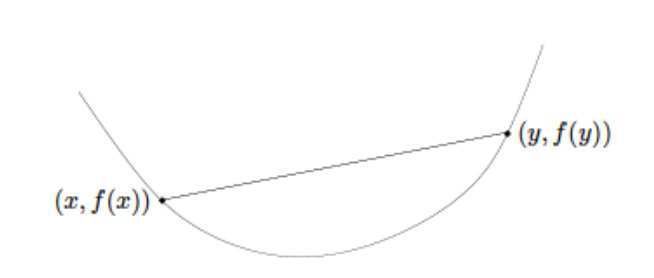
A function f : $R^n \rightarrow R$ is convex if $\forall x, y$ and $\forall \alpha \in [0, 1]$

$f(\alpha x + (1-\alpha) y) \leq \alpha f(x) + (1-\alpha) f(y)$

Convex Hull

Given n points in plane, $S = \{(x_i, y_i)| i = 1,2, ... , n\}$ , Convex Hull(CH(S)): smallest polygon containing all points in S.

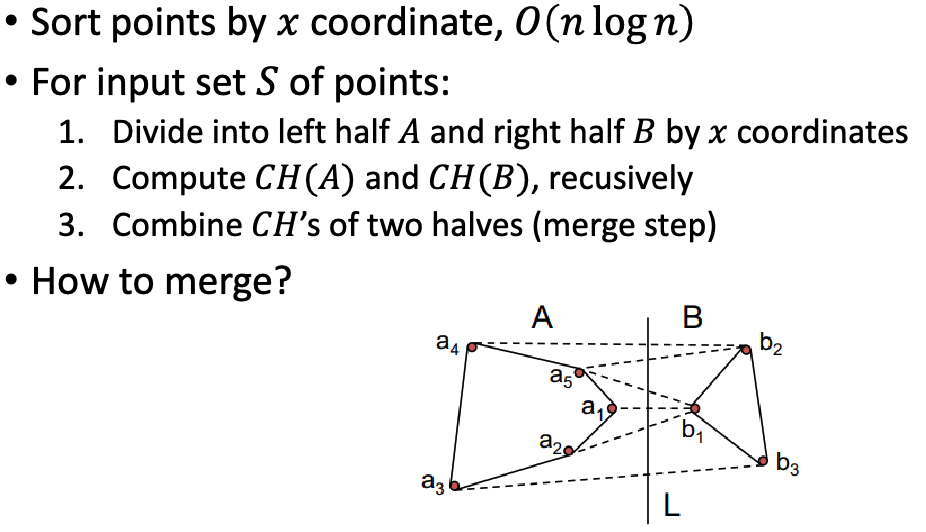
Finding upper tangent, same for lower tangent