4 Probability

Random Variable

A random variable X on a sample space $\Omega$ is a function $X:\Omega\rightarrow R$ that assigns to each sample point $\omega \in \Omega$ a real number $X(\omega)$.

Let a be any number in the range of a random variable X. Then $X(\omega) = a$ is an event in the sample space. We usually abbreivate this event to "X = a".

The distribution of a discrete random variable X is the collection of values $\{(a,P[X = a])\}$, where a $\in$ the set of all possible values taken by X

probability mass function(p.m.f) $P[X=a] = p(a)$

Expectations and Variance

$$E(X) =\sum_{x\in X(\Omega)} xp(x) \\ Var(X) = E[(X - E(X))^2] = E(X^2) - E^2(X)$$

Distribution

X ∼ Bernoulli(p)

one if a coin with heads probability p comes up heads, zero otherwise.

$$\begin{aligned} P[X=i]= \begin{cases} p, & i=1 \\ 1-p, & i=0 \end{cases} \\ E(X)=p \\ Var(X)=p(1-p) \end{aligned}$$

X ∼ Binomial(n, p)

n times Bernoulli experiments

$$\begin{aligned} P[X=i] =( \begin{matrix} n\\i \end{matrix} )p^i(1-p)^{n-i} \qquad \text{i =0,1,...,n}\\ E(X) = np \\ Var(X) = np(1-p) \end{aligned}$$

X ∼ Geometric(p)

For $\lambda > 0$

$$\begin{aligned} P[X = i]= (1− p)^{i-1}p \qquad \text{i = 1,2,3,..} \\ E(X) = \frac{1}{p} \\ Var(X) = \frac{1-p}{p^2} \end{aligned}$$

X ∼ Poisson($\lambda$)

$$\begin{aligned} P[X = i]= \frac{\lambda^i}{i!}e^{-\lambda} \qquad \text{i=0,1,2,...} \\ E(X) = Var(X) = \lambda \end{aligned}$$

Continuous Variable

A probability density function(PDF) for a real-valued random variable X is a function $f:R\rightarrow R$ satisfying

1. $f_X(x) \geq 0$ for all $x \in R$.
2. $\int_{-\infty}^{\infty}f_X(x)dx = 1$

Then the distribution of X is given by $P[a\leq X\leq b] = \int_a^b f_X(x)dx$

cumulative distribution function(CDF) $F_X(x) = P(X\leq x) = \int_{-\infty}^xf_X(z)dz$

$E(x) = \int_{-\infty}^{\infty}xf_X(x)dx$

Distribution

X ∼ Uniform(a, b)

$$f(x) = \begin{cases} \frac1{b-a}, & a\leq x\leq b \\ 0, & other \end{cases}$$

X ∼ Exponential(λ)

For $\lambda > 0$,

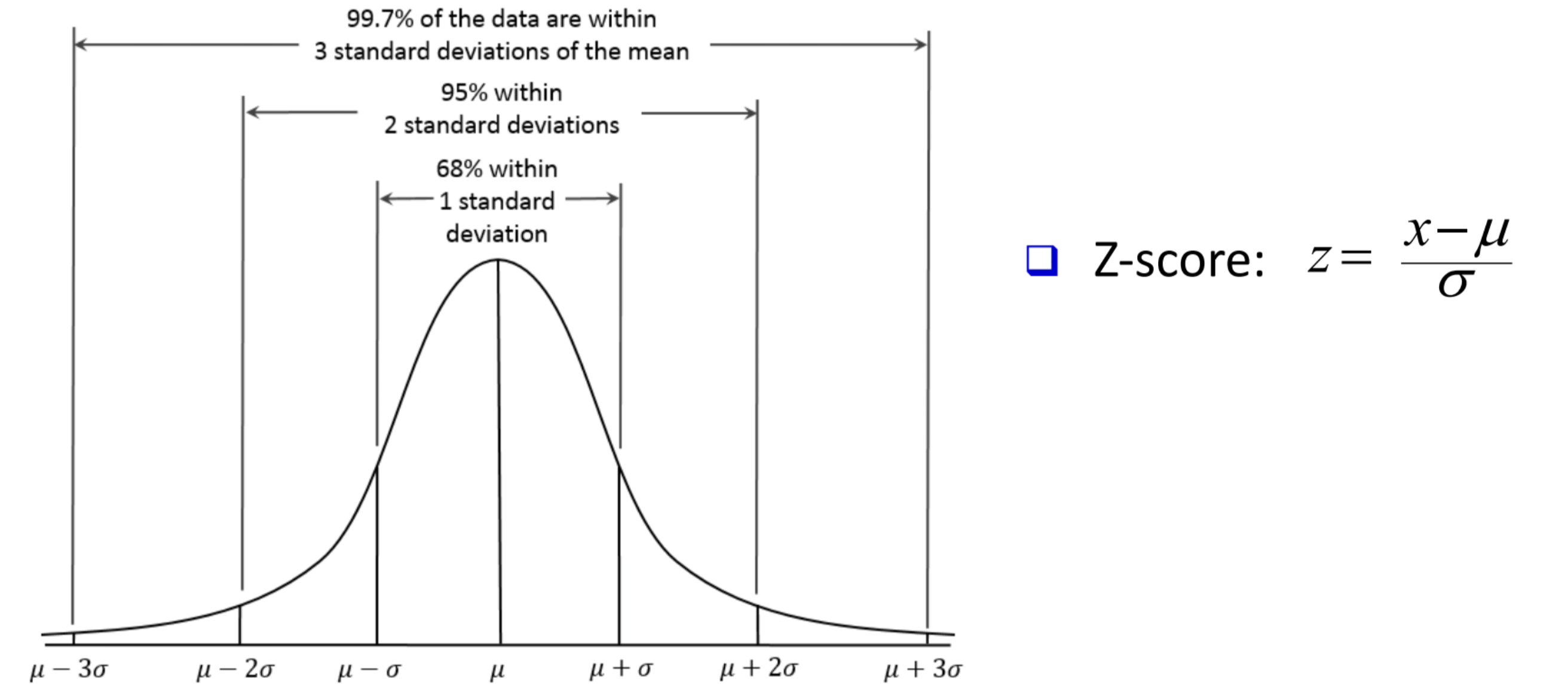
$$f(x) = \begin{cases} \lambda e^{-\lambda x}, & x\geq 0 \\ 0, & other \end{cases}$$

X ∼ Normal($\mu,\sigma^2$)

Also known as the Gaussian distribution

$$f(x) = \frac1{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

Multiple Variables

Joint distribution

Random Joint distribution

For some random variables $X_1,...,X_n$, the joint distribution is written $p(X_1,...,X_n)$

Let $\{X_i\}_{i\in I}$ be a collection of random variables indexed by $I$, which may be infinite. Then $\{X_i\}$ are independent if for every finite subset of indices $i_1,..., i_k \in I$ we have $p(X_{i1},..., X_{ik}) = \prod_{j=1}^kp(X_{ij})$

Marginal distribution $p(X) = \sum_yp(X,y)$

Continuous Joint distribution

For continuous variables, the joint CDF $F_{XY}(x,y) = P(X\leq x, Y\leq y)$

the marginal CDF $F_X(x) = \lim_{y\rightarrow \infty}F_{XY}(x,y)dy$

In the case that $F_{XY}(x, y)$ is everywhere differentiable in both x and y, then we can define the joint PDF $f_{XY}(x,y) = \frac{\partial^2 F_{XY}(x,y)}{\partial x\partial y}$

marginal PDF: $f_X(x) = \int_{-\infty}^{\infty}f_{XY}(x,y)dy$

Conditional Distributions

the conditional PDF $f_{Y|X}(y|x) = \frac{f_{XY}(x,y)}{f_X(x)}$

Covariance

$Cov(X,Y) = E[(X-E(X))(Y-E(Y))] = E(XY) - E(X)E(Y)$

correlation $\rho(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}} \in [-1,1]$

$$\begin{aligned} set Z = (X-E(X))t + (Y-E(Y)) \\ E(Z^2) = Var(X)t^2 + 2Cov(X,Y)t + Var(Y) \geq 0 \\ \Rightarrow 4Cov^2(X,Y) - 4Var(X)Var(Y) \leq 0 \end{aligned}$$

We can define Inner product $\langle X,Y\rangle:=E(XY)$, and correlation as $cos\theta = \frac{\langle X-E(X),X-E(X)\rangle\langle Y-E(Y),Y-E(Y)\rangle}{Var(X)Var(Y)}$

If $\rho^2 = 1$,

$$\begin{aligned} Var(Y-aX) = Var(Y) + a^2Var(X) - 2aCov(X,Y) \\ = Var(Y) + a^2Var(X) - 2a\rho Var(X)Var(Y) \\ = (a\sqrt{Var(X)} - \rho \sqrt{Var(Y)})^2 \end{aligned}$$

if we choose $a = \frac{\rho \sqrt{Var(Y)}}{\sqrt{Var(X)}}$, then $Var(Y-ax) = 0 \Rightarrow Y=aX$

If $\rho = 0$, we say that X and Y are uncorrelated, but that doesn't mean they are independent.

if X ∼ Uniform(−1, 1) and $Y = X^2$ , then one can show that X and Y are uncorrelated, even though they are not independent.

For multiple variables, define covariance matrix. It is symmetric and semi-definite (for any x, $x^T\Sigma x \geq 0$)

$$\Sigma = E[(X-E(X))(X-E(X))^T] = \left[ \begin{matrix} Var(X_1) & Cov(X_1, X_2) & \cdots & Cov(X_1, X_n)\\ Cov(X_2, X_1) & Var(X_2) & \cdots & Cov(X_2, X_n)\\ \vdots & \vdots & \ddots & \vdots\\ Cov(X_n, X_1) & Cov(X_n, X_2)& \cdots & Var(X_n) \end{matrix} \right]$$

Independence

Two random variables X and Y are independent if $F_{XY}(x, y) = F_X(x)F_Y(y)$ for all values of x and y. Equivalently,

• For discrete random variables, $p(x,y) = p(x)p(y)$
• For continuous variables, $f_{XY}(x, y) = f_X(x)f_Y(y)$

The Gaussian distribution

$p(x; \mu, \Sigma) = \frac1{\sqrt{(2\pi)^d \det{\Sigma}}}{\exp(-\frac12(x-\mu)^T\Sigma^{-1}(x-\mu))}$

Estimation of Parameters

Maximum Likelihood estimation

We make some assumptions about our problem by prescribing a parametric model, then we fit the parameters of the model to the data. How do we choose the values of the parameters?

A common way to fit parameters is maximum likelihood estimation(MLE).

Suppose we have random variables $X_1, . . . , X_n$ and corresponding observations $x_1, . . . , x_n$. Then likelihood function

$L(\theta) = p(x_1, . . . , x_n;\theta)$

We assume $X_1, . . . , X_n$ are independent. Then

$$\begin{aligned} L(\theta) = \prod_{i=1}^np(x_i;\theta)\\ \log L(\theta) = \sum_{i=1}^n\log p(x_i;\theta) \\ \theta _{mle} = \arg\max L(\theta) \end{aligned}$$

Information Theory

Entropy

Information: How uncertain we are of the outcome of random experiments

Self information: $i(x) = - \log_2p(x)$

Entropy

$$\begin{aligned} H(X) = E[i(x)] = -\sum_{x\in X(\Omega)}p(x)\log_2p(x) \\ H(X,Y) = -\sum_{y\in y(\Omega)}\sum_{x\in X(\Omega)}p(x,y)\log_2p(x,y) \\ H(X|Y) = -\sum_{y\in y(\Omega)}\sum_{x\in X(\Omega)}p(x,y)\log_2p(x|y) \\ H(X,Y) = H(X) + H(Y|X) = H(Y) + H(X|Y) \end{aligned}$$

Relative Entropy

Jensen's inequality: Let X be a random variable and f(x) be a convex function, then

$$E(f(X))\geq f(E(X))$$

Conversely, if f(x) is a concave function

$$E(f(X))\leq f(E(X))$$

Relative Entropy (Kullback-Leibler divergence):

$$D(p(x)||q(x)) = \sum_{x\in X(\Omega)}p(x)\log\frac{p(x)}{q(x)} = - E_p[\log\frac{q(x)}{p(x)}] \geq -\log E_p[\frac{q(x)}{p(x)}] \geq 0$$

Connection to MLE

Set loss function loss$(x) = -\log q(x)$, the expect value would be

Risk$(q) = -E_p(\log q(x))= D(p||q) +$ Risk$(p)$

Thus, $\arg \min D(p||q) = \arg \min$ Risk$(q)$

Here, we call Risk(q) as cross entropy CE(p,q)