2 Graph

Graph

Definition

Graph: 𝐺 = (𝑉, 𝐸)

V: set of vertices.
$E\subseteq V\times V$ (set of edges)

if $e=\lbrace u,v\rbrace\in E$ and $u=v$ , we call e as "loop"

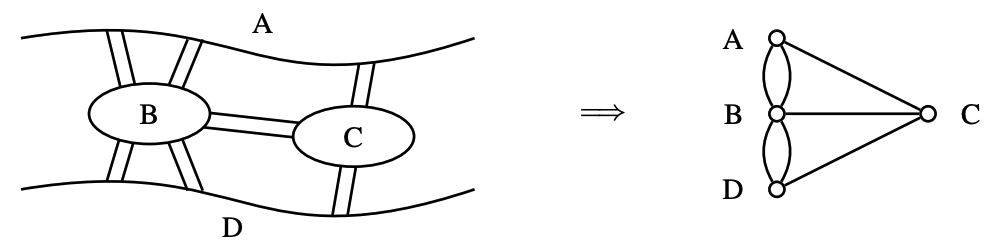
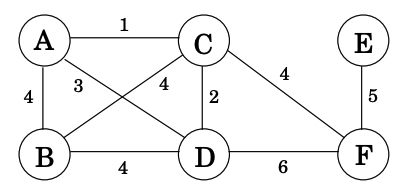
In Figure 1, V = {A,B,C,D} and E = {{A,B},{A,B},{A,C},{B,C},{B,D},{B,D},{C,D}}.

Here, E is a multiset.

If there are no loops and E is a set(no parallel edges), then G is a simple graph.

u is neighbor of v if $\lbrace u,v\rbrace \in E$ , edge $\lbrace u,v\rbrace$ is incident to u and v.
Degree of vertex u is number of incident edges

20221105110711

In directed graph, each $e\in E$ defined as $(u,v)$ .

the in-degree of a vertex u is the number of edges from other vertices to u, and the out-degree of u is the number of edges from u to other vertices.

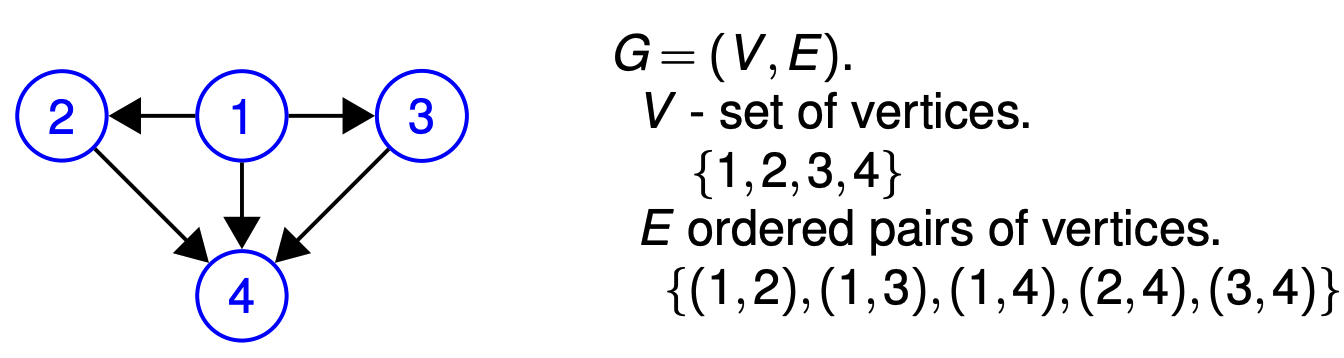
20221105112539

Paths, walks, cycles, tour

Path: a sequence of edges $(v_1,v_2),(v_2,v_3),...,(v_{k-1},v_k)$
Cycle: Path from $v_1$ to $v_{k-1}$ , + edge $(v_{k-1},v_1)$
Walk is sequence of edges with possible repeated vertex or edge
Tour is walk that starts and ends at the same node.

Hamiltonian cycle: A cycle that visits every vertex in graph exactly once

Connectivity

u and v are connected if there is a path between u and v

Connected graph: A graph where all pairs of vertices are connected
Connected component: Maximal set of connected vertices
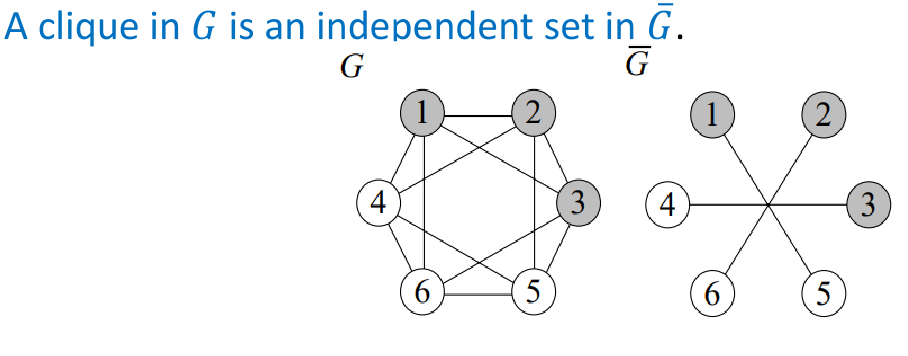
Independent set: No two vertices are connected by an edge
Clique: Every pair of vertices is connected by an edge
Minimum Vertex Cover: for every edge $(u, v) \in E$ , either $u \in V'$ or $v \in V'$ . The task is to find the minimum $|V'|$

20240507151659

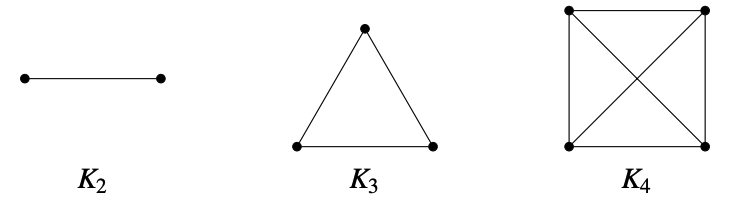
Complete Graph

$K_n$ complete graph on n vertices

every pair of (distinct) vertices u and v are connected by an edge $\lbrace u,v\rbrace$ .

20221105155349

Representation

Adjacency matrices are true if there is a line going from node A to B and false otherwise
Adjacency lists list out all the nodes connected to each node in our graph

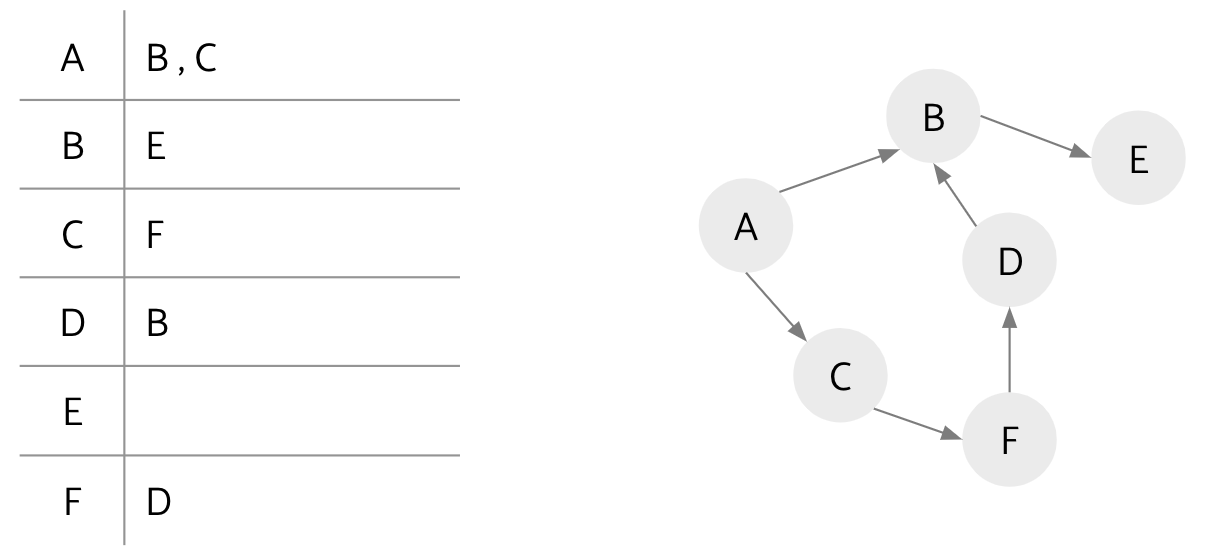
Searching

DFS and BFS runtime with adjacency list: O(V + E) (creating marked array)

DFS and BFS runtime with adjacency matrix: O( $V^2$ )

DFS is worse for spindly graphs (Θ(V) memory to remember recursive calls)

BFS is worse for absurdly “bushy” graphs (In worst case, queue will require Θ(V) memory.)

Bipartite

An undirected graph 𝐺 = (𝑉, 𝐸) is bipartite if you can partition the vertex set into 2 parts so that all edges join vertices in different parts

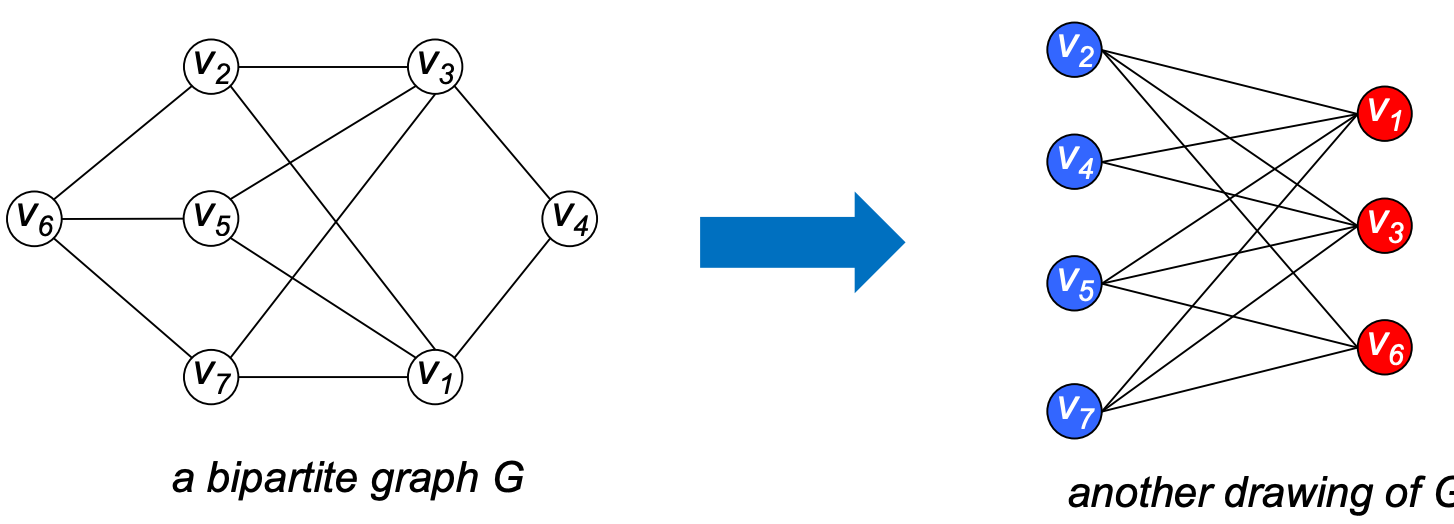
20230601211523

A graph G is bipartite if and only if it contains no odd length cycles.

Proof:

(1) If G is bipartite, then it does not contain an odd length cycle.

20230601211637

(2) Let G be a connected graph, and let $L_0,... , L_k$ be the layers produced by BFS.

Then only 2 situations:

No edge of G joins two nodes of the same layer, and G is bipartite. See blue and red parts.
An edge of G joins two nodes of the same layer, and G contains an odd-length cycle (and hence is not bipartite). Consider the edge and the lowest common ancestor of the connecting vertices. The total length must be odd.

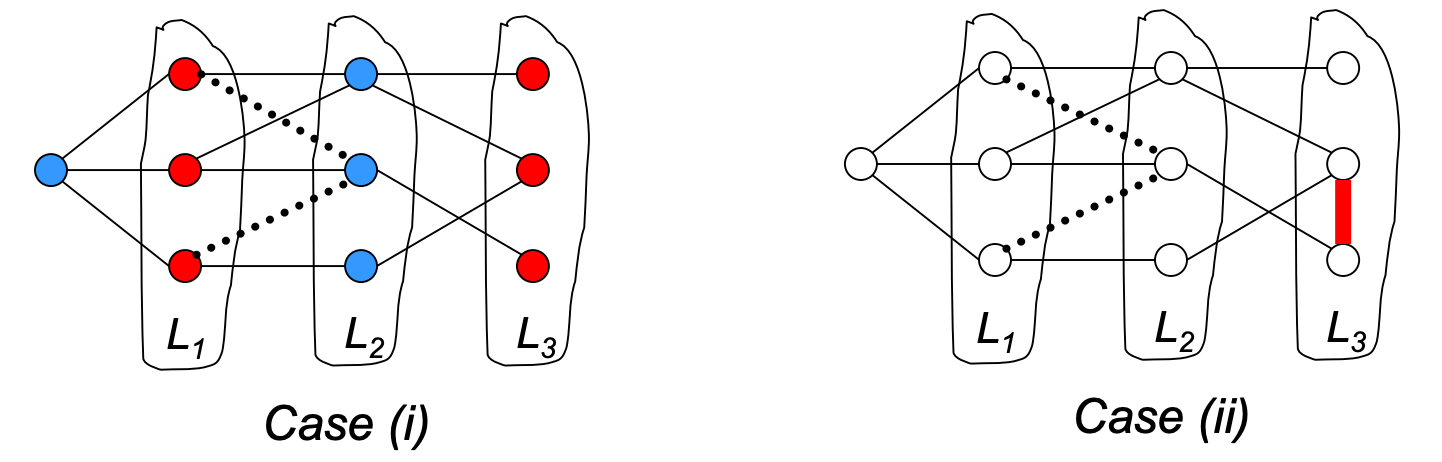
20230601211746

tip

BFS solution to test bipartiteness:

队首孩子结点入队时, 判断是否在同一层

Shortest Path

Dijkstra's algorithm /ˈdaɪkstrə/

int dijkstra(){
    PQ.push({source, 0});
    while(!PQ.empty()){
        p = PQ.top();
        PQ.pop();
        for (q:adjlist[p]){
            if (distTo[p] + w < distTo[q]){
                distTo[q] = distTo[p] + w; // relax
                edgeTo[q] = p;
                PQ.push({q, distTo[q]});
            }
        }
    }
}

Dijkstra’s is guaranteed to return a correct result if all edges are non-negative

Proof:

After relaxing all edges from source, let vertex v1 be the vertex with minimum weight(closest to the source)

Claim: distTo[v1] is optimal, and thus future relaxations will fail

distTo[p] ≥ distTo[v1] for all p, therefore
distTo[p] + w ≥ distTo[v1]

Runtime:

removeSmallest: V times, each costing O(log V) time.
changePriority: E times, each costing O(log V) time.

Assuming E > V, this is just O(Elog V) for a connected graph

DAG

Directed acyclic graph

Topological sort: order the vertices one after the other in such a way that each edge goes from an earlier vertex to a later vertex

A topological sort only exists if the graph is a DAG

Property: Every dag has at least one source and at least one sink(proof easy)

O(V+E) time
Θ(V) space

Solution

process all of the edges and keep a count of the number of incoming edges for each node
Find a source, output it, and delete it from the graph
The graph is still a DAG, and thus will still have a source vertex
Repeat until the graph is empty

bool topolical_sort(){
    // graph可包含self cycle and parallel edge
    queue<int> q;
    // find source
    for (int i = 0; i < indegree.size(); ++i) {
        if (!indegree[i]) q.push(i);
    }
    // repeating pop source
    while (!q.empty()) {
        int u = q.front();
        res.push_back(u);
        q.pop();
        for (auto v: graph[u]){
            --indegree[v];
            if (!indegree[v]) q.push(v);
        }
    }
    // Check DAG
    return res.size()==n;
}

Shortest path on DAG

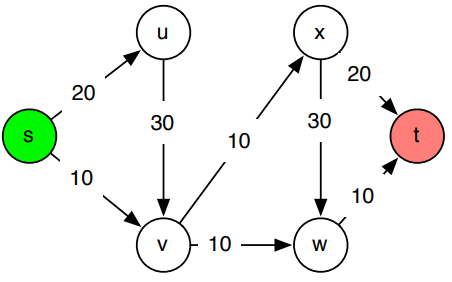
Dijkstra may suffer from negative edges(dist to 5 is update earlier than 2)

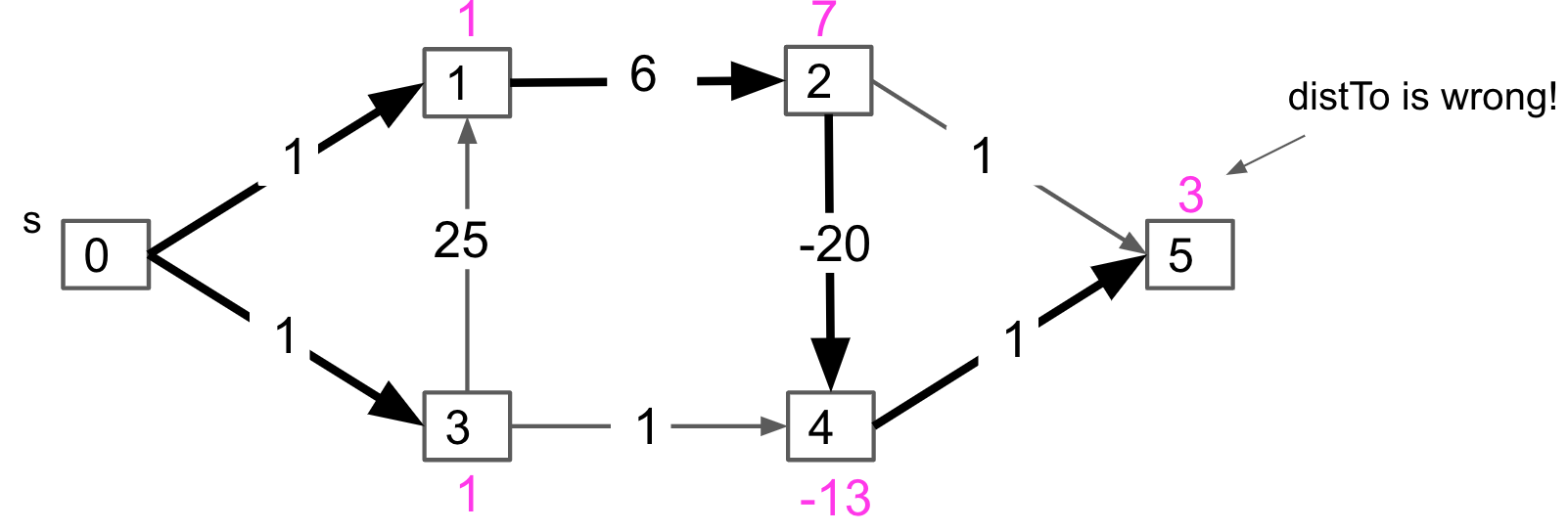
20221209223906

Solution: visit all the vertices in topological order, relaxing all edges as we go

O(V+E) time
Θ(V) space

Longest path on DAG: just flip all weights and treat as SPT

Tree

A connected graph without a cycle

or: A connected graph with |V| −1 edges.

Binary Tree

Tree Terminology

The depth of a node is the number of edges from the root to the node
The height of a node is the number of edges from the node to the deepest leaf
The height of a tree is a height of the root
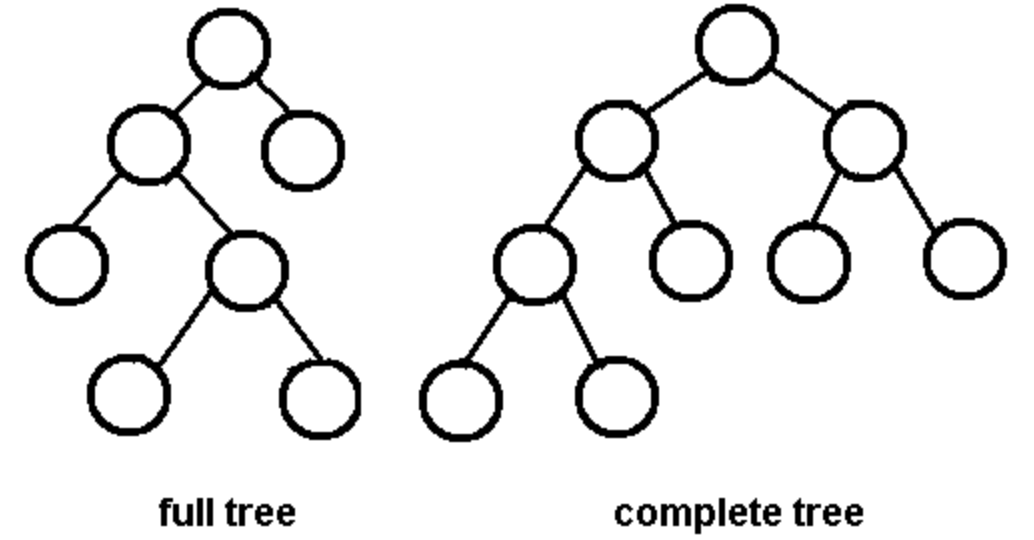
A full binary tree is a binary tree in which each node has exactly zero or two children
A complete binary tree is a binary tree, which is completely filled, with the possible exception of the bottom level, which is filled from left to right

20230524152640

Tree traversals

A traversal is a process that visits all the nodes in the tree

depth-first traversal
- PreOrder traversal
- InOrder traversal
- PostOrder traversal
breadth-first traversal
- For binary tree, BFS = level order traversal

BST

Binary search in ordered linked list

Move pointer to middle and flip left links

20221128220141

Binary Search Tree

20221128220221

A BST is a binary tree where nodes are ordered in the following way:

Every key in the left subtree is less than X's key
Every key in the right subtree is greater than X's key

insert

insert(BST T, Key ik) {
    if (T == null)
        return new BST(ik);
    if (ik ≺ T.key)
        T.left = insert(T.left, ik);
    else if (ik ≻ T.key)
        T.right = insert(T.right, ik);
    return T;
}

delete

Deletion with two Children(Hibbard)

If we want to delete k, move g or m upward

20221128221020

Implement Map

To represent maps, just have each BST node store key/value pairs

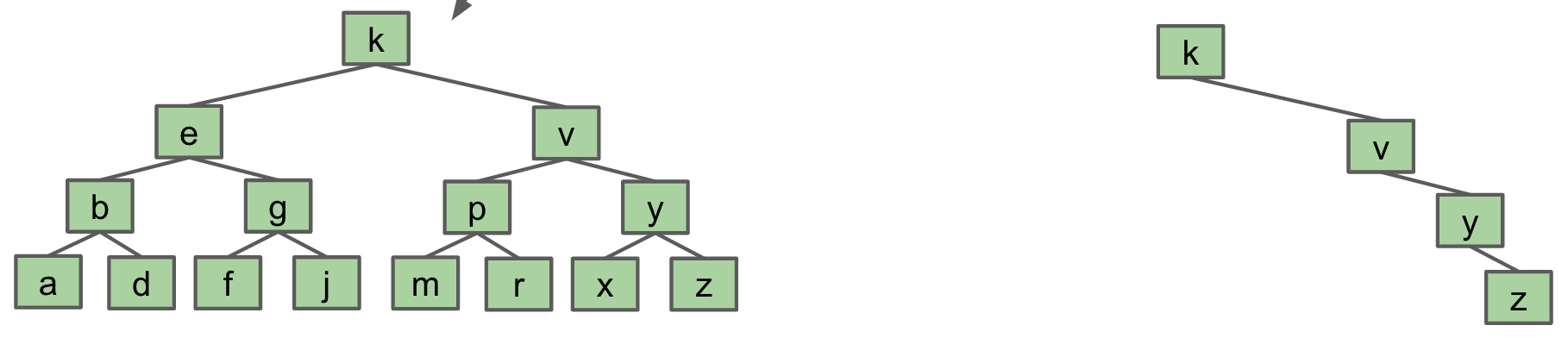
Tree Height

Θ(log N) in the best case (Left: "bushy")
Θ(N) in the worst case (Right: "spindly")
Θ(log N) height if constructed via random inserts

20221128222035

BST Rotation

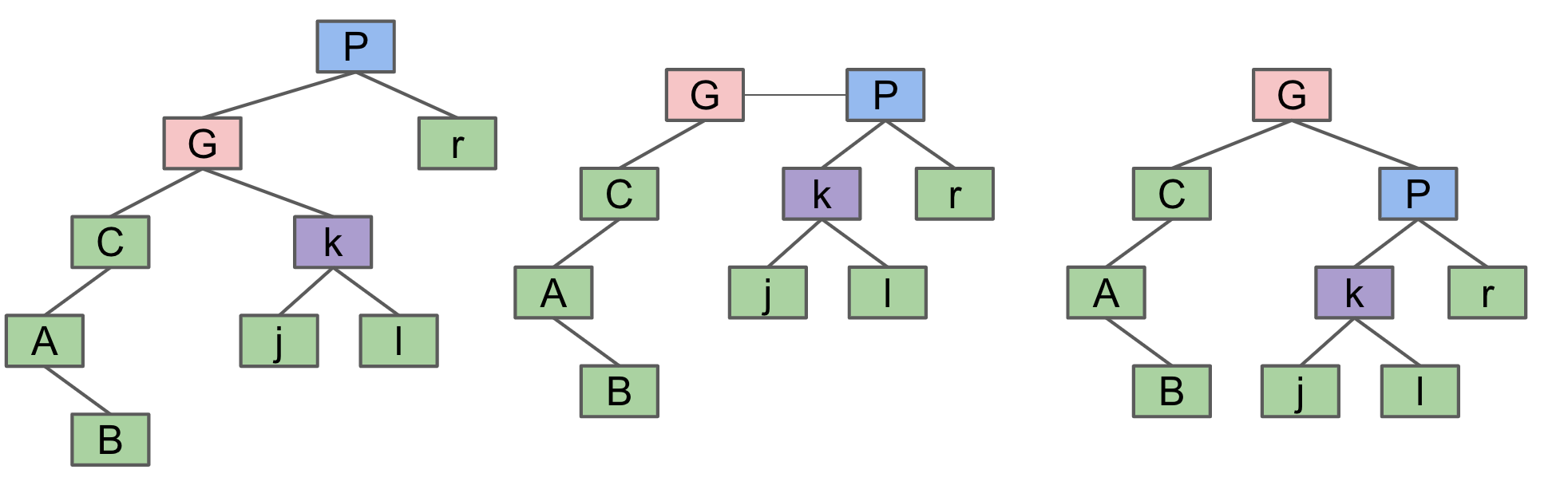
rotateLeft(G): Head->Left Child

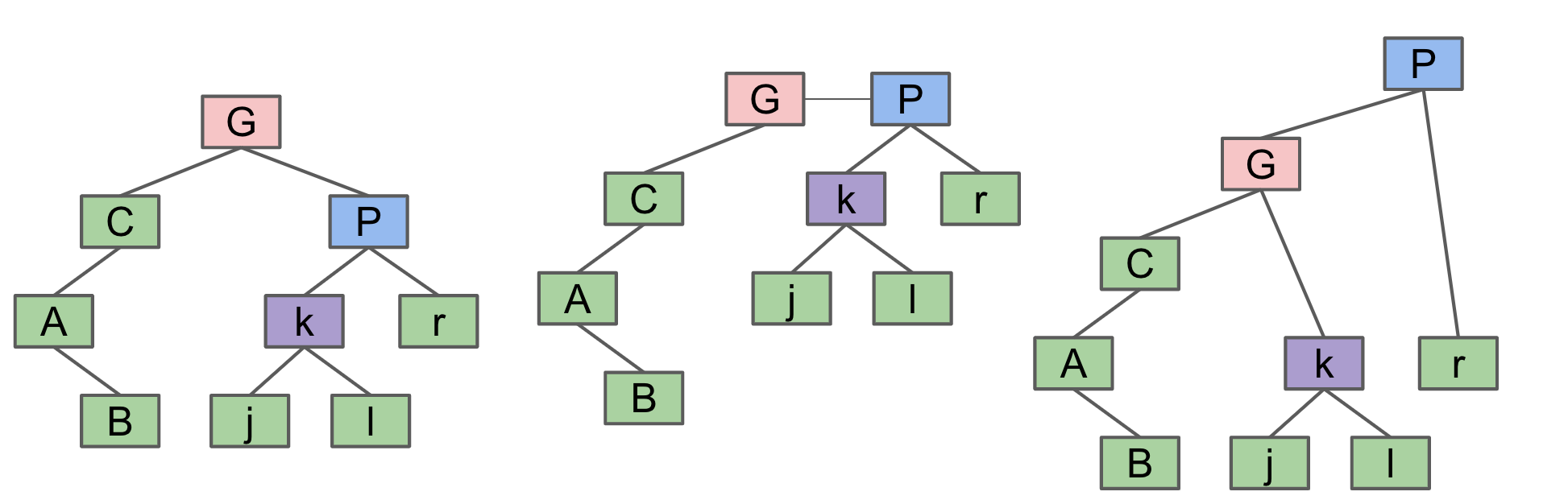
20221202112028

rotateRight(P): Head->Right Child

20221202112721

Rotation:

Can shorten (or lengthen) a tree
Preserves search tree property

BTree

Concept

Problem with BST: Adding new leaves at the bottom makes it imbalanced -> Avoid new leaves by "overstuffing" the leaf nodes

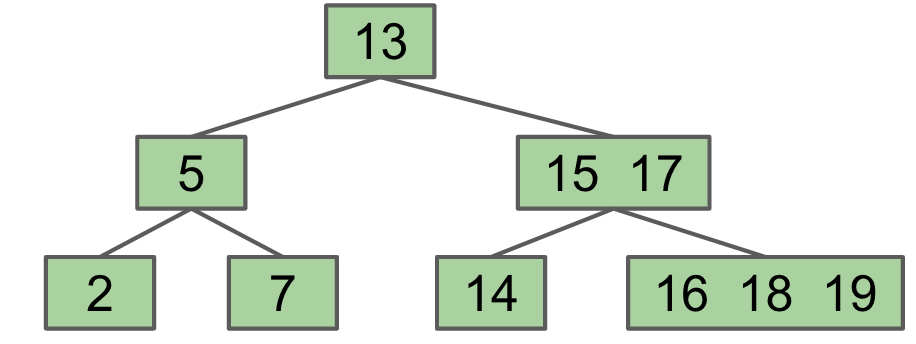
20221201211741

Height is balanced, but leaf nodes can get too juicy

Solution: Set a limit L on the number of items, say L=3, move the left-middle

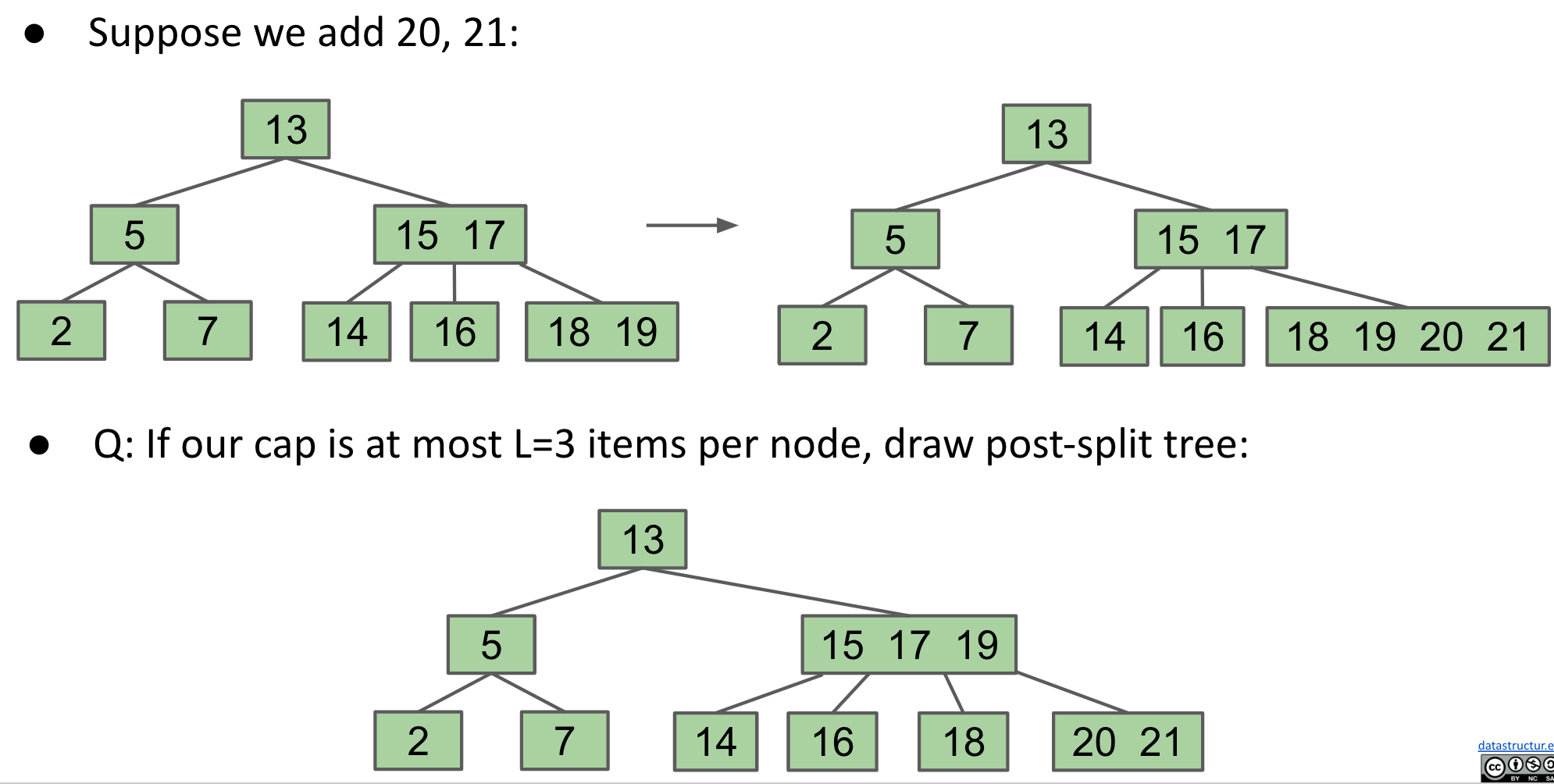
20221201212635

B(balanced/bushy)-trees of order L=3 are also called a 2-3-4(number of children) tree or a 2-4 tree

B-Tree Runtime Analysis

The minimum degree of the B-tree t is an integer such that:

Every node other than the root must have at least t - 1 keys
Every internal node other than the root must have at least t children
The root must have at least one key

Height:

\begin{aligned} n \geq 1 + (t-1)\sum_{i=1}^H 2t^{i-1} \geq 1 + 2(t^H -1) \geq 2t^H -1 \\ H \leq \log_t{(n+1)/2} \end{aligned}

H = O(log n)

Contains:

Worst case number of nodes to inspect: H + 1
Worst case number of items to inspect per node: L
Overall runtime: O(HL) = O(log n)

Add:

Worst case number of nodes to inspect: H + 1
Worst case number of items to inspect per node: L
Worst case number of split operations: H + 1
Overall runtime: O(HL) = O(log n)

Red-Black Trees

Representing a 2-3 Tree as a BST

Binary search trees: Can balance using rotation
2-3 Tree: Balanced by construction

Solution: Create "glue"(red) links with the smaller item off to the left

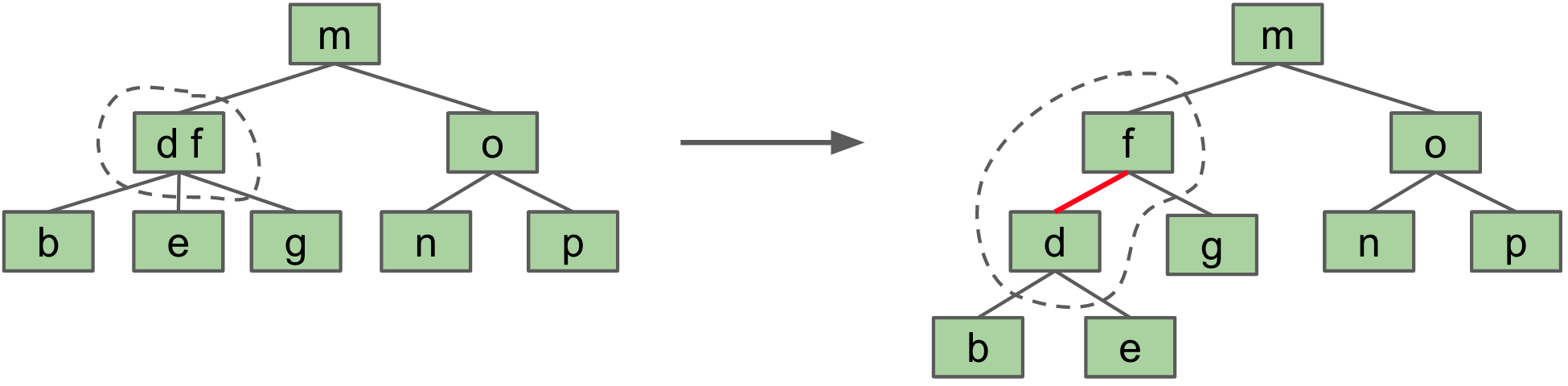
20221202113356

Left-Leaning Red Black Binary Search Tree (LLRB)

There is a 1-1 correspondence between an LLRB and an equivalent 2-3 tree

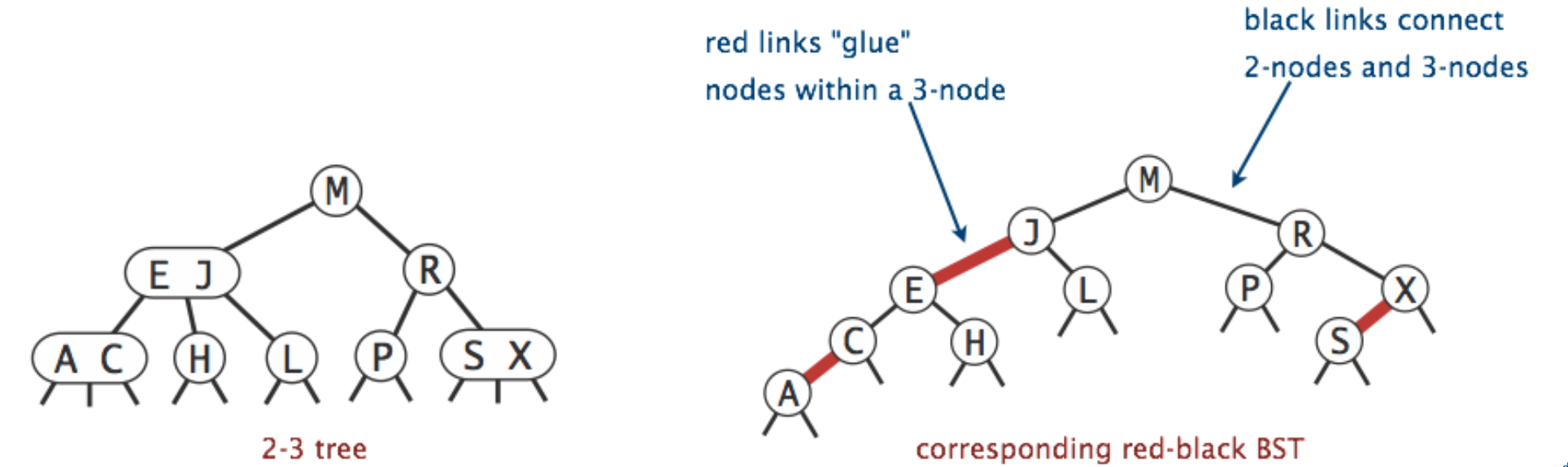
20221202113510

private class Node {
    private Key key;           // key
    private Value val;         // associated data
    private Node left, right;  // links to left and right subtrees
    private boolean color;     // color of parent link
    private int size;          // subtree count

    public Node(Key key, Value val, boolean color, int size) {
        this.key = key;
        this.val = val;
        this.color = color;
        this.size = size;
    }
}

LLRB Height

LLRB has no more than ~2x the height of its 2-3 tree: O(log n)

Insertion

Use red link

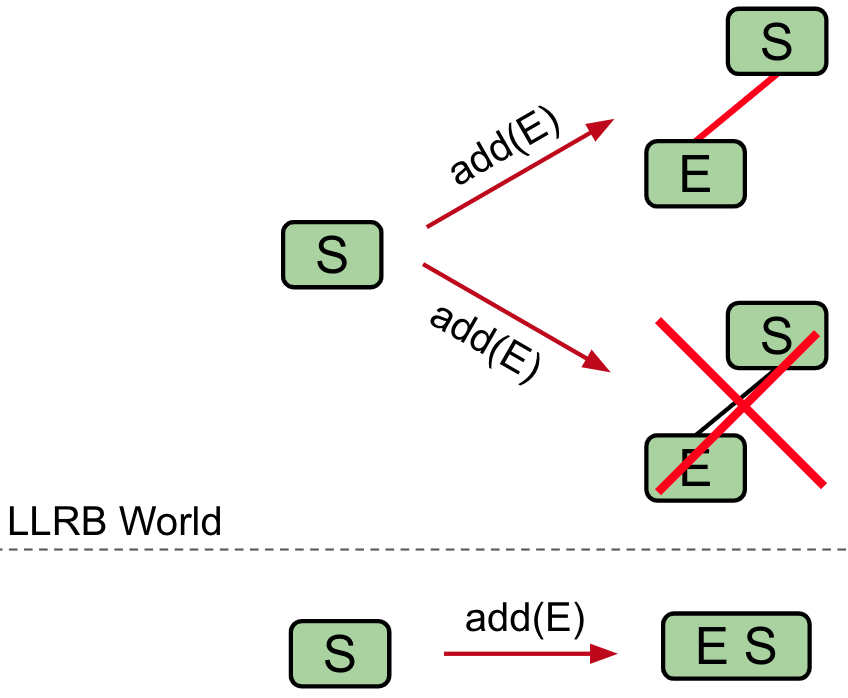
20221202114204

Insertion on the Right

If there is a right leaning "3-node", Rotate left the appropriate node to fix

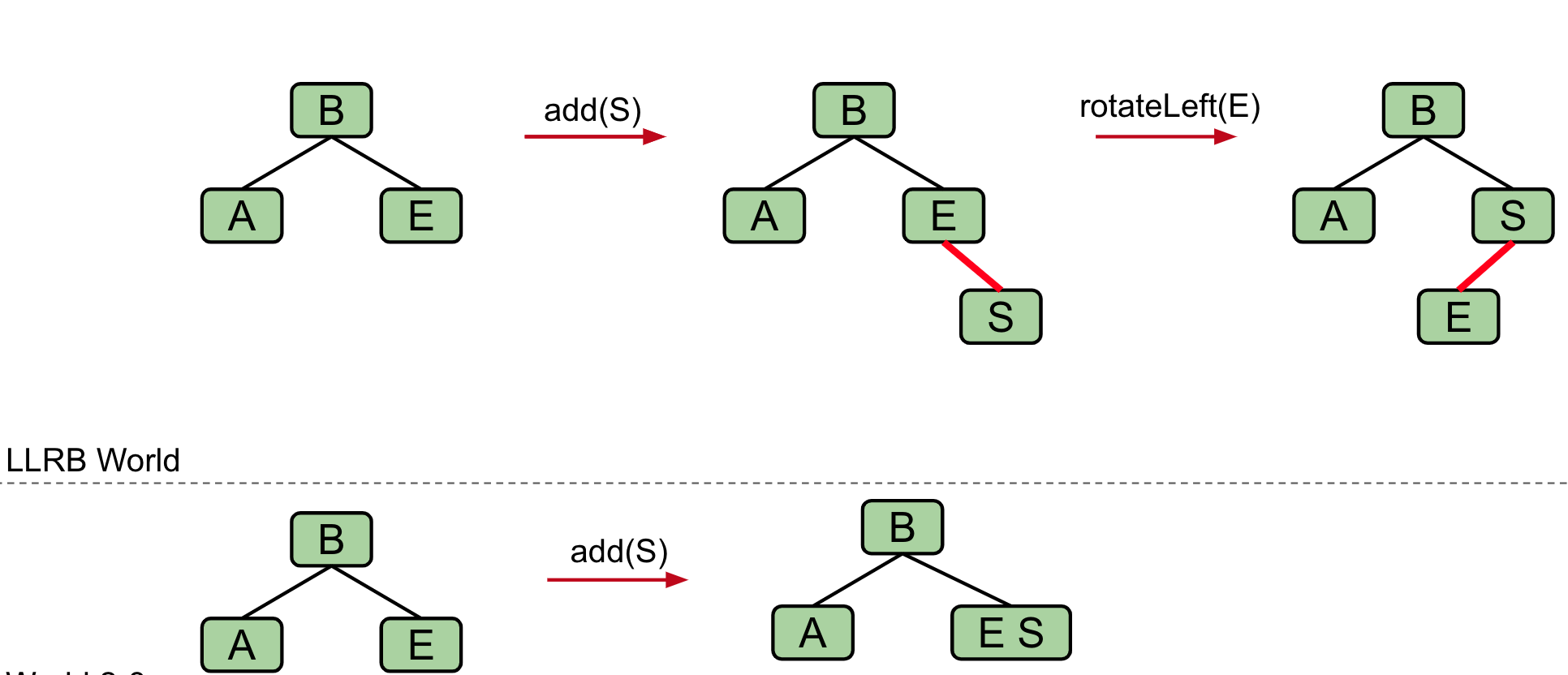
20221202114424

private Node rotateLeft(Node h) {
    assert (h != null) && isRed(h.right);
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    x.color = h.color;
    h.color = RED;
    x.size = h.size;
    h.size = size(h.left) + size(h.right) + 1;
    return x;
}

Double Insertion on the Left

If there are two consecutive left links, rotate right the appropriate node to fix

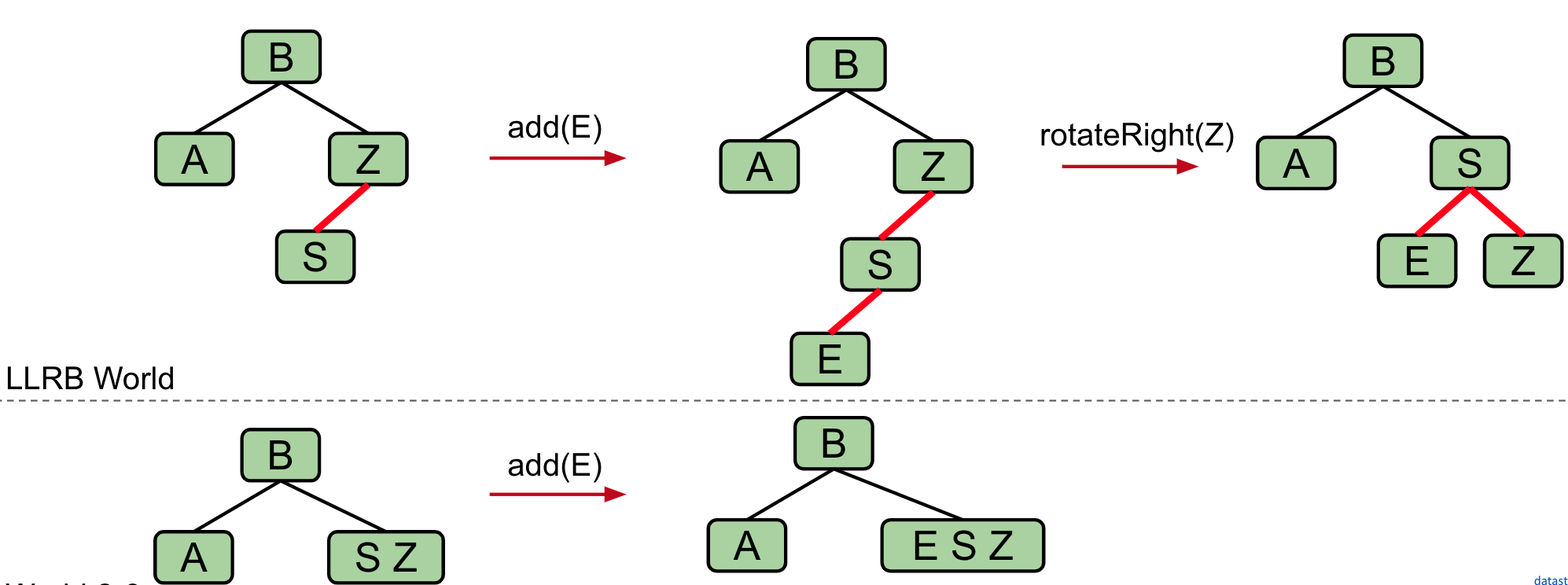
20221202115012

private Node rotateRight(Node h) {
    assert (h != null) && isRed(h.left);
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = h.color;
    h.color = RED;
    x.size = h.size;
    h.size = size(h.left) + size(h.right) + 1;
    return x;
}

Splitting 4-Nodes

If there are any nodes with two red children, color flip

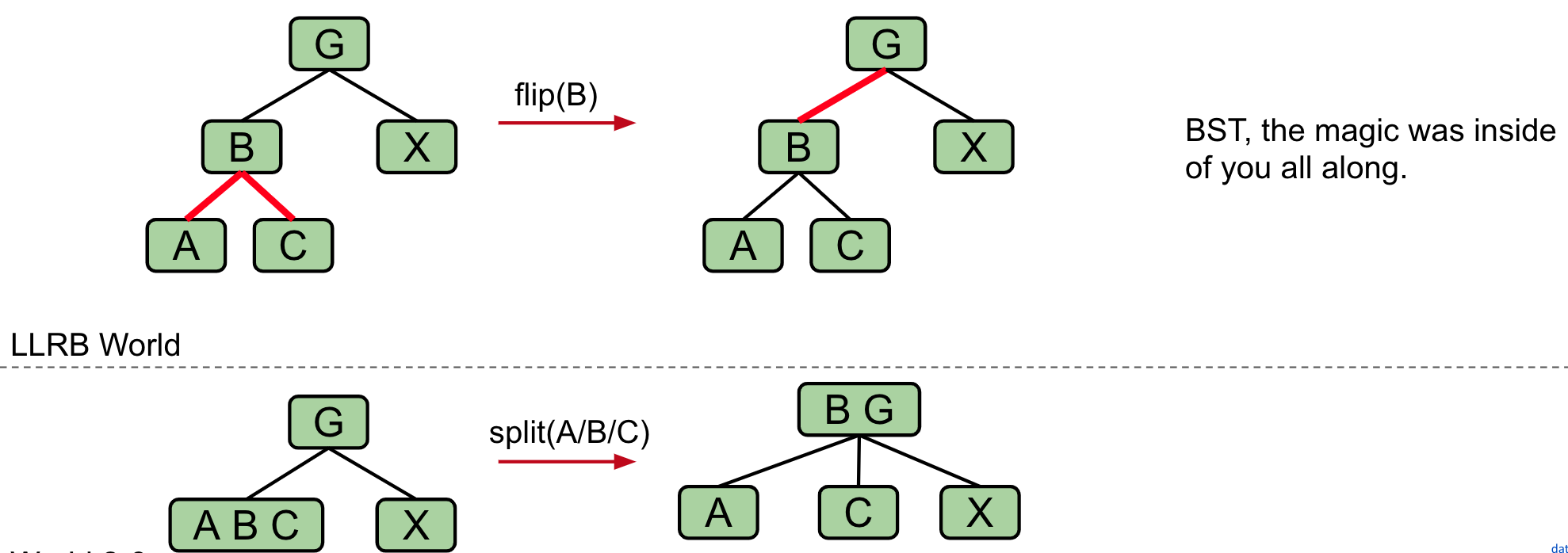
20221202115231

private void flipColors(Node h) {
    h.color = !h.color;
    h.left.color = !h.left.color;
    h.right.color = !h.right.color;
}

Cascading operations

It is possible that a rotation or flip operation will cause an additional violation that needs fixing

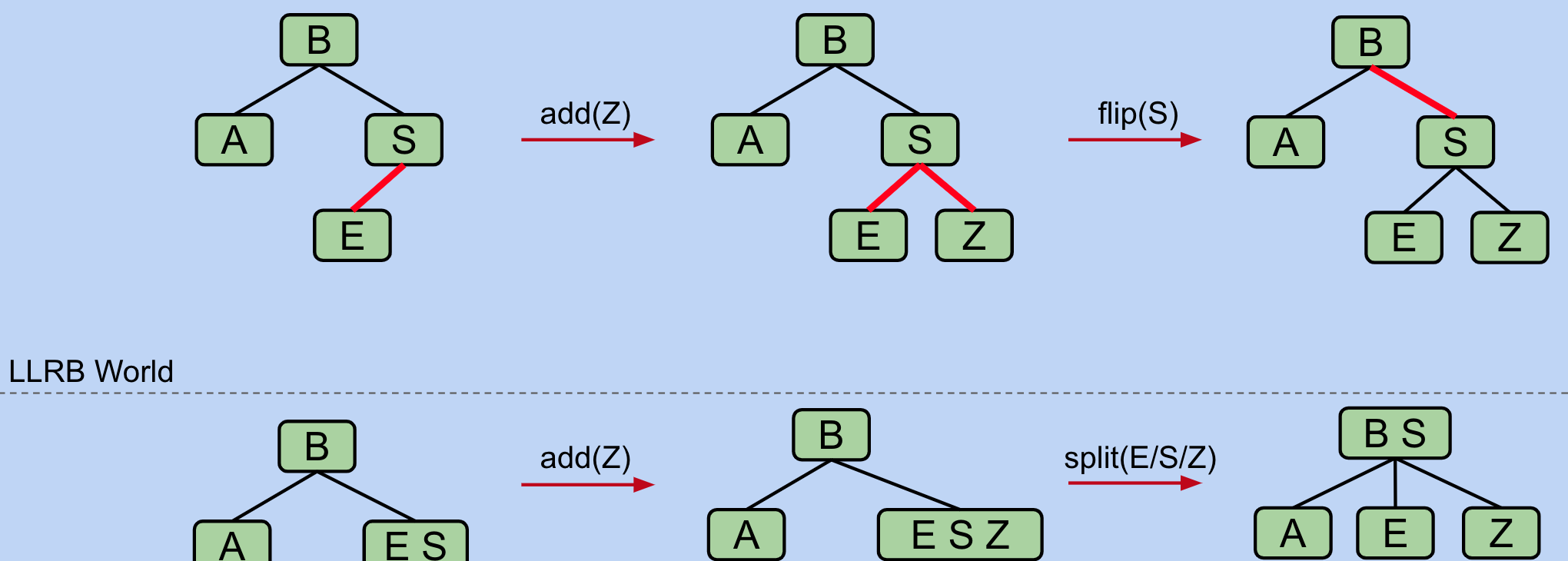
20221202115843

Wrapping it up

private Node put(Node h, Key key, Value val) {
    if (h == null) return new Node(key, val, RED, 1);

    int cmp = key.compareTo(h.key);
    if      (cmp < 0) h.left  = put(h.left,  key, val);
    else if (cmp > 0) h.right = put(h.right, key, val);
    else              h.val   = val;

    // fix-up any right-leaning links
    if (isRed(h.right) && !isRed(h.left))      h = rotateLeft(h);
    if (isRed(h.left)  &&  isRed(h.left.left)) h = rotateRight(h);
    if (isRed(h.left)  &&  isRed(h.right))     flipColors(h);
    h.size = size(h.left) + size(h.right) + 1;

    Balance(); // Cascading operations
    return h;
}

LLRB Runtime

Contains: O(log n)
Insert:
- O(log n) to add the new node
- O(log n) rotation and color flip operations per insert

Disjoint Sets

int findf(int v){
    if(v!=father[v])
        father[v]=findf(father[v]);//注意点
    return father[v];
}
void uni(int a,int b){
    int fa = findf(a);
    int fb = findf(b);
    if(fa!=fb)
        father[fa] = fb;
}

Improvement: Weighted Quick Union

Modify uni():

Track tree size (number of elements)
Always link root of smaller tree to larger tree

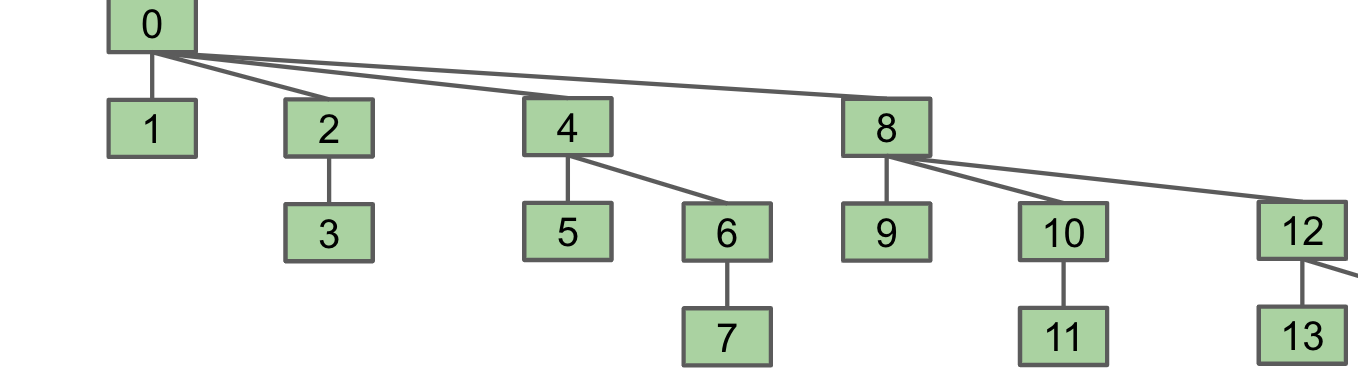
20221203164944

Worst case tree height is O(log n)

$\Rightarrow$ findf and uni are O(log n)

Minimum Spanning Trees

Input: An undirected graph G = (V, E), edge weights $w_e$

Output: A tree $T = (V, E')$ , with $E_0 \subset E$ , that minimizes weight $(T) = \sum_{e\in E'}w_e$

20221105161941

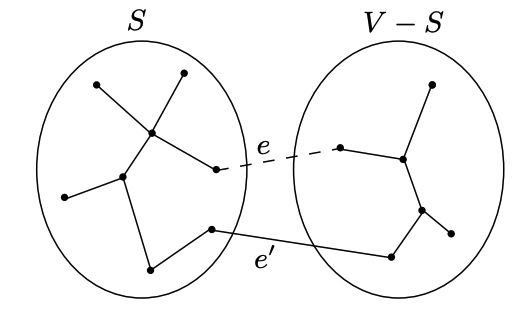
Cut property

A cut is any partition of V into two groups, S and V −S

A crossing edge is an edge which connects a node from S to a node from the V-S

Claim: Given any cut, minimum weight crossing edge is in the MST

Proof:

Suppose a minimum spanning tree $T$ doesn't contain e, then there must be some other edge $e'$ across the cut (S, V −S)

if we remove $e'$ and add $e$ , $T' = T \lbrace e\rbrace − \lbrace e'\rbrace$ , then T' must be connected.

And it has the same number of edges as T; so it is also a tree.

but weight $(T')\leq$ weight $(T)$

20221105164746

Prim's Algorithm

Prim Runtime just as Dijkstra: O(ElogV)

int prism(){
    distTo[s] = 0;
    PQ.push({s,0})
 
    /* Get vertices in order of distance from tree. */
    while (!PQ.empty()) {
        int v = PQ.top();
        PQ.pop();
        visit[v] = true;
        for (Edge e:adjlist[v]){
            int q = e.head;
            if (!visit[q] && e.weight < distTo[q]) {
                distTo[q] = e.weight;
                edgeTo[q] = e;
                PQ.push({q, distTo[q]});
            }
        }
    } 
}

Kruskal's Algorithm

int kruskal(){
    sort(EdgeList.begin(),EdgeList().end());
    for(e:EdgeList){
        int fa = findf(e.from);
        int fb = findf(e.to);
        if(fa!=fb){
            father[e.from] = e.to;
            edgeTo[e.to] = e;
        }
    }
}

Runtime:

sort: O(ElogE)
union: O(ElogV)

Assuming E > V, this is just O(ElogE)

Network Flow

Definition

A flow network is a connected, directed graph G = (V, E).

Each edge $e$ has a capacity $c_e > 0$
A single source $s \in V$ and a single sink $t \in V$
No edge enters the source and no edge leaves the sink

Def. A flow is a function $f:E\rightarrow R^+$ that assigns a real number to each edge, satisfying the following two properties

Capacity: $0 \leq f(e)\leq c_e$ for each edge e
Conservation: $f^{in}(u) = f^{out}(u)$ for each vertex except s,t

capacity of the cut: cap(A,B) = $\sum_{\text{e leaving A}}c_e$

Our task is to maximize the value of the flow $v(f) = f^{out}(s)$

20240306113519

Flow and Cut Lemma

Flow Lemma: Let f be any flow, and let (A, B) be any s-t cut. Then

$v(f) = f^{out}(A) - f^{in}(A)$ (Proof Easy) $\Rightarrow v(f) = f^{in}(t)$

Cut capacity Lemma: Let f be any flow, and let (A, B) be any s-t cut. Then the value of the flow is at most the capacity of the cut.

$v(f)\leq$ cap(A,B)

Residual graph

Residual graph $G^f = (V, E^f)$

For an origin edge e = (u, v) in G

Remaining capacity left: if $f_e < c_e$ , copy the edge e with capacity $c_e - f_e$
Erase origin: if $f_e > 0$ , include an edge e' = (v, u) with capacity $f_e$

Augmenting Path:

Let P be an s − t path in the residual graph $G_f$
Let bottleneck (P, f) be the smallest capacity in $G_f$ on any edge of P
We can increase the flow by (P, f)

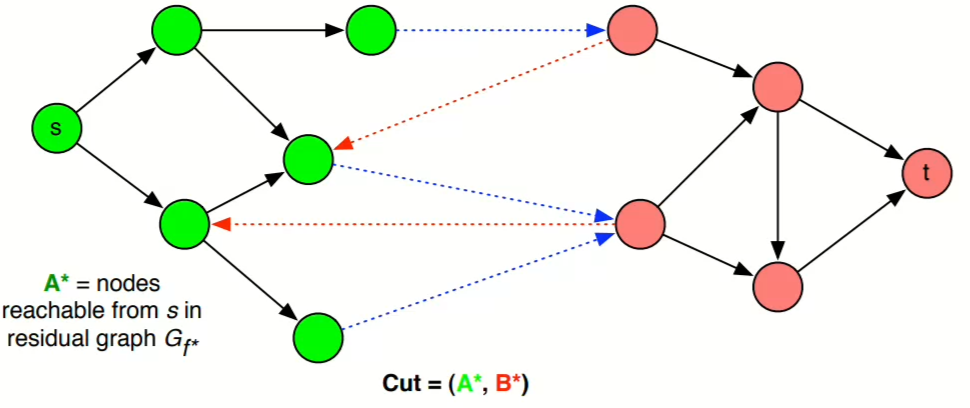
Theorem: maximum flow = minimum cut

Proof: if $f^*$ is maximized, then $G_{f^*}$ has no augmenting path

Let $A^*$ denote the set of vertices that are reachable from s: If there is an augmenting path from s to a vertex v then $v \in S$ . Also $t\in B^*$

Blue edges must be saturated otherwise there would be a forward edge which make an augmenting path
Red edges must be empty otherwise there would be a forward edge which make an augmenting path

$v(f^*) = f^{out}(A^*) - f^{in}(A^*) = cap(A^*,B^*)$

20240306214613

Algorithms

Ford-Fulkerson Algorithm

Runtime: O((E+V)f)

Assuming E > V, this is O(Ef)

int dfs(int s, int t, int flow){
    visit[s] = true;
    for (Edge e:adjlist[s]){
        if(e.weight > 0 && !visit[e.from]){
            int newFlow = dfs(e.to, t, min(flow, e.weight));
            if(newFlow > 0){
                e.weight -= newFlow;
                edge[e.to].weight += newFlow;
                return newFlow;
            }
        }
    }
    return -1;
}
int ff(int s, int t){
    int ans = 0;
    while (1)
    {
        memset(visit, false, sizeof(visit));
        int d = dfs(s, t, inf);
        if (d == -1)
            return ans;
        ans += d;
    }
}

2 Graph

Graph​

Definition​

Paths, walks, cycles, tour​

Connectivity​

Complete Graph​

Representation​

Searching​

Bipartite​

Shortest Path​

DAG​

Directed acyclic graph​

Solution​

Shortest path on DAG​

Tree​

Binary Tree​

BST​

insert​

delete​

Implement Map​

Tree Height​

BST Rotation​

BTree​

Concept​

B-Tree Runtime Analysis​

Red-Black Trees​

LLRB Height​

Insertion​

Insertion on the Right​

Double Insertion on the Left​

Splitting 4-Nodes​

Cascading operations​

LLRB Runtime​

Disjoint Sets​

Minimum Spanning Trees​

Prim's Algorithm​

Kruskal's Algorithm​

Network Flow​

Definition​

Flow and Cut Lemma​

Residual graph​

Algorithms​

Ford-Fulkerson Algorithm​

Graph

Definition

Paths, walks, cycles, tour

Connectivity

Complete Graph

Representation

Searching

Bipartite

Shortest Path

DAG

Directed acyclic graph

Solution

Shortest path on DAG

Tree

Binary Tree

BST

insert

delete

Implement Map

Tree Height

BST Rotation

BTree

Concept

B-Tree Runtime Analysis

Red-Black Trees

LLRB Height

Insertion

Insertion on the Right

Double Insertion on the Left

Splitting 4-Nodes

Cascading operations

LLRB Runtime

Disjoint Sets

Minimum Spanning Trees

Prim's Algorithm

Kruskal's Algorithm

Network Flow

Definition

Flow and Cut Lemma

Residual graph

Algorithms

Ford-Fulkerson Algorithm