1 Regression and Classification

Classification vs Regression:

• The target variables in classification are discrete, while in regression are continuous
• Classes have their order, while Clusters are exchangeable

Notations and general concepts

L-norm

Minkowski distance(L-norm)

def minkowski_distance(a, b, p):
 return sum(abs(e1-e2)**p for e1, e2 in zip(a,b))**(1/p)

• p = 1, Manhattan Distance
• p = 2, Euclidean Distance

Normalization

• Z score(See probability)
• Min - max

Batch Normalization

Internal Covariate Shift(ICS)

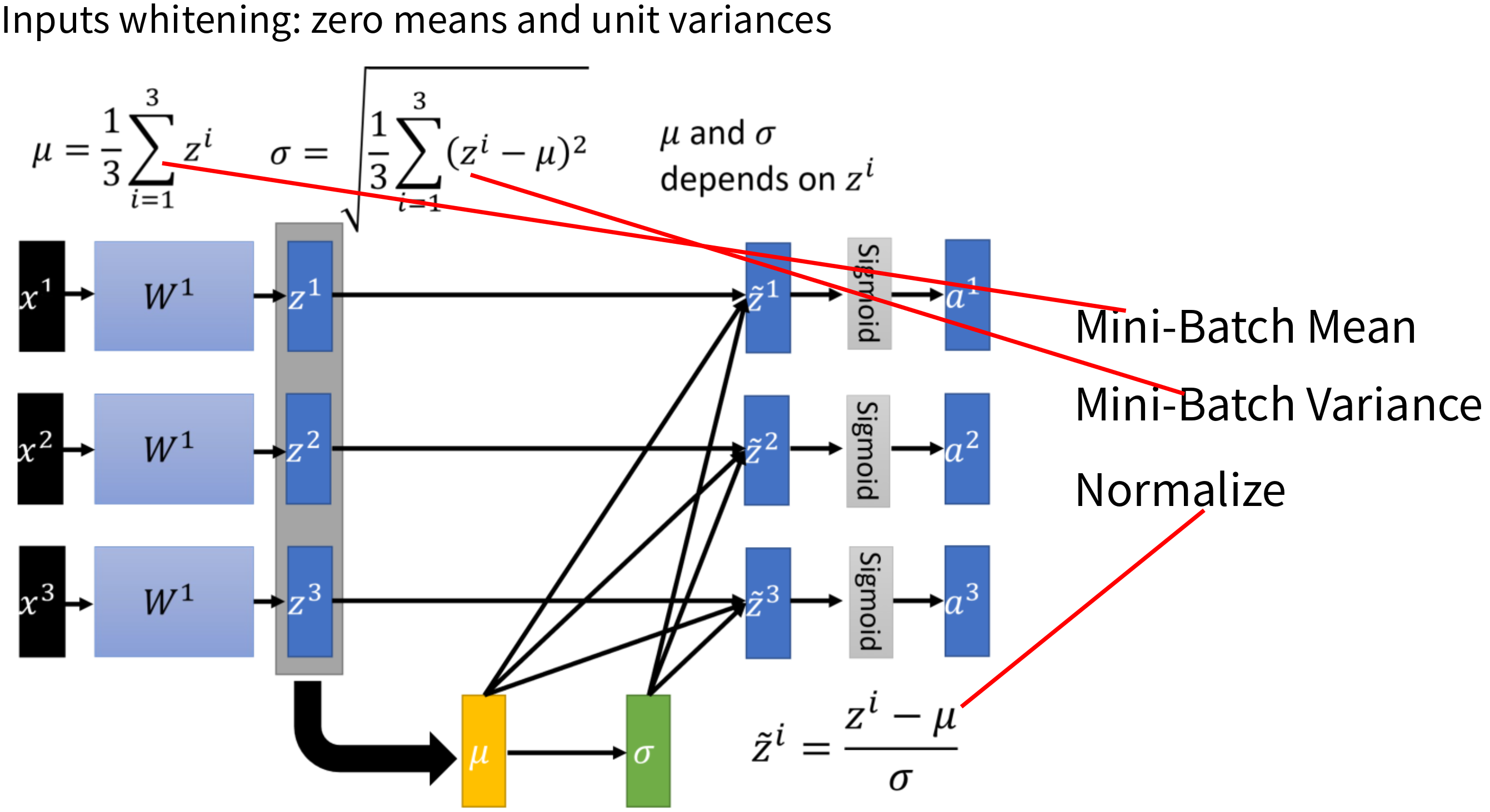
• While training a model, we expect independent and identically distributed data
• For a deep learning model, as the parameter of a lower layer changes, the input distribution of the upper layer also changes. It's called Internal Covariate Shift
• The upper layer's parameters need to continuously adapt to the new input data distribution, thus reduces the learning speed

Problems caused by ICS

• Require Lower learning rates: Training would be slower
• More careful about initializing: saturated regime will slow down the convergence

Batch normalization

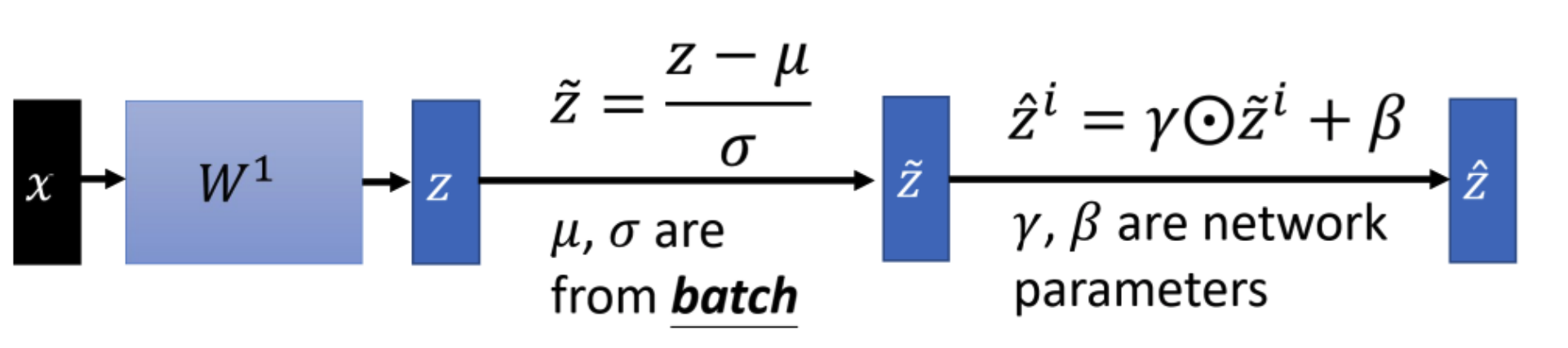
• Batch normalize: Calculate mini-batch mean and variance of each layer to decrease covariate shift
• Scale and shift: Identity transform in order to avoid linear regime of the nonlinearity

Layer Normalization

Compute the layer normalization all the hidden units in the same layer

Cross Validation

simple cross validation:

1. Randomly divide training data into $S_{train}$ and $S_{cv}$(cross validation)
2. For each model, traing on $S_{train}$
3. Estimate error on validation set $S_{cv}$
4. find the smallest error

K fold cross validation:

1. Randomly divide training data into k equal parts $S_1,S_2,...,S_k$
2. For each model, traing on all the data except $S_j$
3. Estimate error on validation set $S_j$: $error_{S_j}$
4. Repeat k times, find the smallest error

$Error = \frac1k \sum_{i=1}^k error_{S_j}$

Leave-one-out cross validation:

repeatedly train on all but one of the training examples and test on that held-out example

K fold vs LOO:

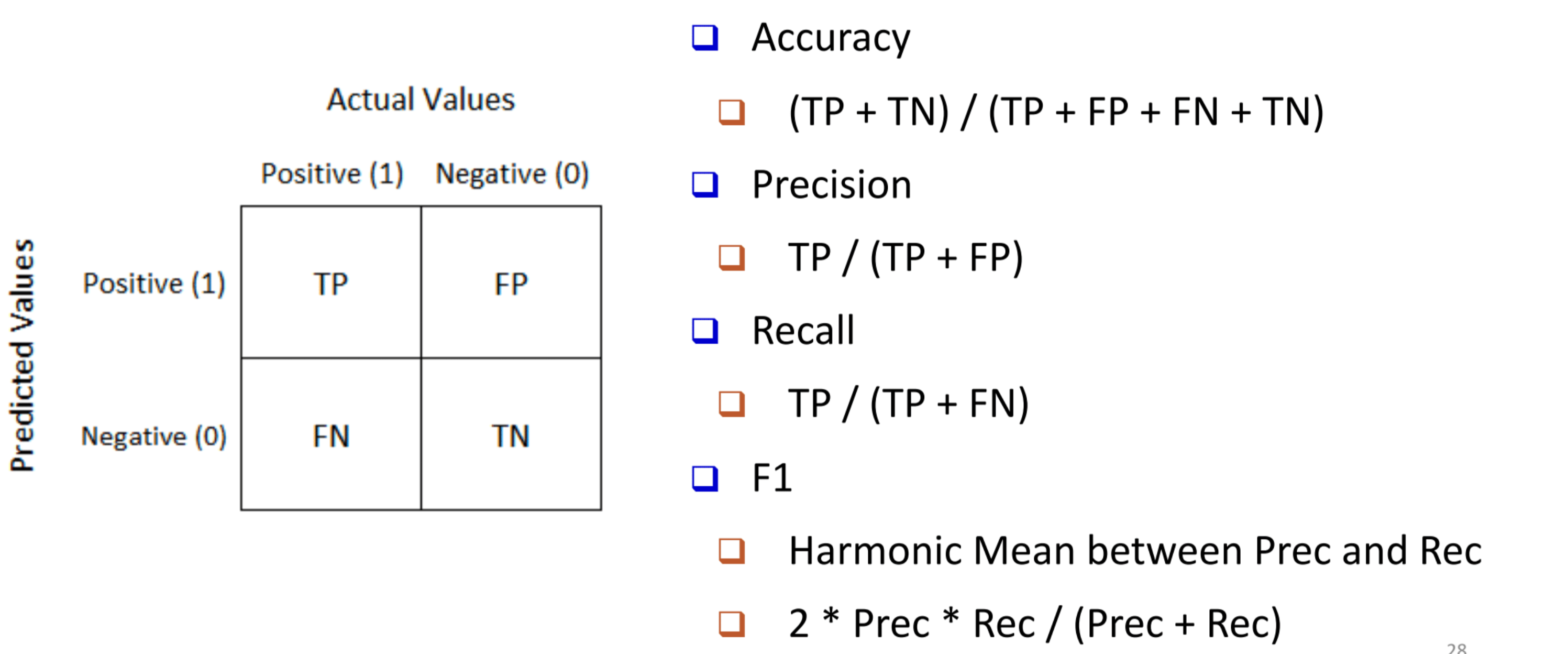
• much faster
• more biased(LOO used in sparse dataset)

Metrics

• Precision: the proportion of correctly predicted positive instances out of all instances the model predicted as positive. $\text{Precision}_i = \frac{\text{TP}_i}{\text{TP}_i + \text{FP}_i}$
• Recall: the proportion of correctly predicted positive instances out of all actual positive instances. $\text{Recall}_i = \frac{\text{TP}_i}{\text{TP}_i + \text{FN}_i}$
• $\text{Macro F1} = \frac{1}{n} \sum_{i=1}^{n} \text{F1}_i$, $\text{Macro Precision} = \frac{1}{n} \sum_{i=1}^{n} \text{Precision}_i$
• $\text{Micro Precision} = \frac{\sum_c TP_c}{\sum_c TP_c + \sum_c FP_c}$, $\text{Micro Recall} = \frac{\sum_c TP_c}{\sum_c TP_c + \sum_c FN_c}$

Linear Regression

Say we find a function $f(x,\theta) = \theta^T x$

minimize a loss function $L(\theta) = \sum_{i=1}^Nl(f(x^{(i)},\theta),y^{(i)})$

Ordinary Least Square Regression

• $\theta: \omega,b$
• $l$: square loss

$L = \frac12\sum_{i=1}^N(f(x^{(i)},\theta) - y^{(i)})^2$ ($\frac12$ 为了gradients约分)

Gradient descent

For square loss,

$$\nabla_{\theta} L(\theta_t) = \frac{\partial L(\theta)}{\partial \theta_j} = x_j(y-h_{\theta}(x))$$

1. Initialize $\theta_0$ randomly, t = 0
2. Repeat: $\theta_{t+1} = \theta_{t} - \eta \nabla_{\theta} L(\theta_t)$, t = t+1

$\eta$ is the learing rate

• too small: no much progress
• too big: Overshoot

Adjust Learning rate

• constant learning rate
• linear decay: linearly decreases over the training period
• cosine learning rate: a max learning rate times the cosine value(from 0 to 1)
• adaptive learning rate

Adagrad:

$$\begin{aligned} \eta_t = \frac{\eta}{\sqrt{t+1}}, g_t = \nabla_{\theta} L(\theta_t) \\ \theta_{t+1} = \theta_t - \frac{\eta_t}{\sigma^t}g_t \\ \sigma_t = \sqrt{\frac{\sum_{i=0}^{t}g^2_i}{t+1}} \end{aligned}$$

Stochastic Gradient Descent

Gradient descent could be slow: Every update involves the entire training data

Stochastic Gradient Descent (SGD)

Sample a batch of training data to estimate $\nabla L(\theta_t)$

Classification

Assume in C1, $X \sim N(\mu_1,\sigma^2)$; in C2, $X \sim N(\mu_2,\sigma^2)$

Apply min-max normalization for the target variable $\rightarrow$ [0,1]

Bayes‘ rule:

$$P(C_1|x) = \frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1) + P(x|C_2)P(C_2)}$$

we can proof that Logistic Regression

$$\log\frac{P(C_1|x)}{P(C_2|x)} = \theta^T x$$

As

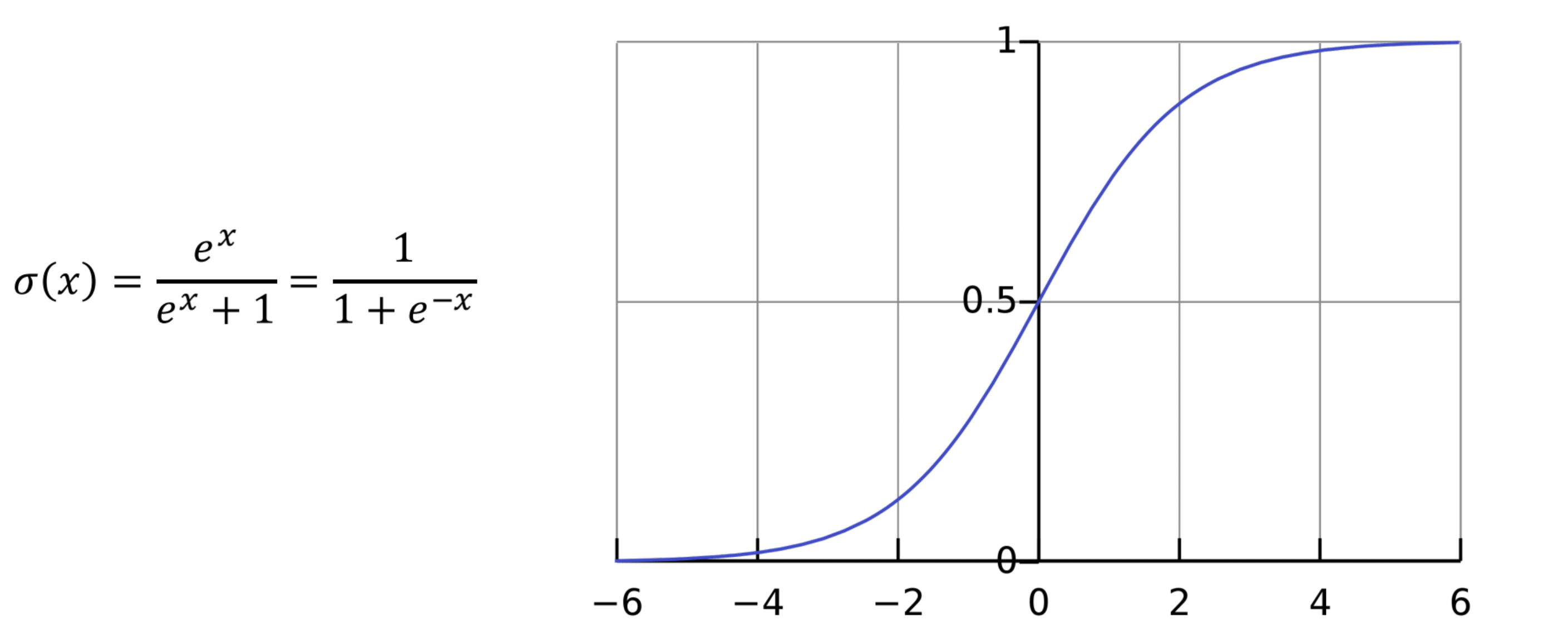
$$\begin{aligned} P(C_1|x) + P(C_2|x) = 1 \\ P(C_1|x) = \frac1{1+e^{-{\theta}^Tx}} = \frac1{1+e^{-z}} \end{aligned}$$

We called it "Sigmoid"

Maximum Likelihood Estimate

Let us assume that $P(y|x;\theta)=h_{\theta}(x)$, $y_i=\{0,1\}$

$$p(x_1,x_2,...,x_n;\theta) = \prod_{i=1}^n h_{\theta}^{y_i}(x_i)(1-h_{\theta}(x_i))^{1-y_i}$$

Cross-Entropy Loss

$$L(\theta) = \log p(x_1,x_2,...,x_n;\theta) = \sum_{i=1}^n y_i\log h_{\theta}(x_i) + (1-y_i)\log (1-h_{\theta}(x_i))$$

Then

$$\frac{\partial L(\theta)}{\partial \theta_j} = x_j(y-h_{\theta}(x))$$

same as gradient descent

Multiclass Classification

If we look at sigmoid function $P(y_1|x) = \frac{e^{\theta^Tx}}{e^{\theta^Tx} + 1}$, we could extend the dimension and proof that

$$P(y|x;\theta) = \frac{\exp(\vec{\theta^T x})}{\sum_{j=1}^n\exp(\theta_j^Tx)}$$

We define softmax: softmax$(t_1, . . . , t_k) = \frac{\exp(\vec{t})}{\sum_{j=1}^n\exp(t_j)}$

In fact, that's the same as

$$p(y_i|x) = \frac{p(x|y_i)p(y_i)}{\sum_jp(x|y_j)p(y_j)}$$

We could also proof that MLE loss is the same as cross entropy CE$(y,\hat y)$

$$\mathcal{L}_{NLL} = - \frac{1}{m} \sum_{i=1}^m \sum_{y \in Y_i} \log P(y \mid x_i; \theta)$$

$$\mathcal{L}_{CE} = - \frac{1}{m} \sum_{i=1}^m \sum_{j=1}^n y_{ij} \log P(y_j \mid x_i; \theta)$$