1 Number Representation

Number Representation

Unsigned

$\sum_{i=0}^{w-1} x_i2^i$

Signed-Magnitude

"first" bit gives sign, rest treated as unsigned (magnitude)

Biased Notation

The actual value is the binary value plus a fixed bias

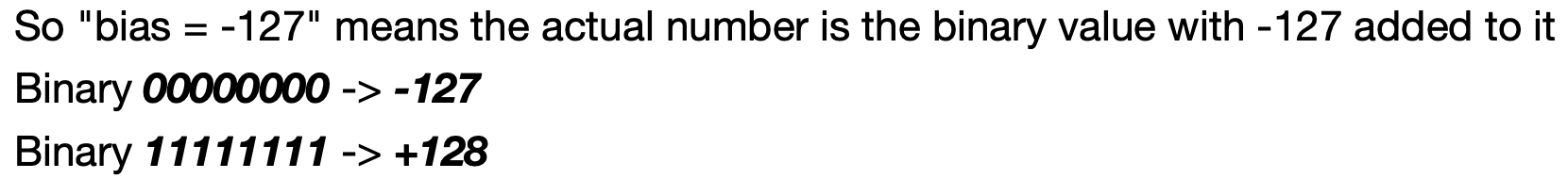
Two’s Complement

$-x_{w-1}2^{w-1}+\sum_{i=0}^{w-2} x_i2^i$

Logical Operations

Shift operations

• Left Shift: throw away extra bits on left, fill with 0's on the right
• Right Shift: throw away extra bits on right
  • logical shift: fill with 0's on the left
  • arithmetic shift: replicate most significant bit(x >> k gives$\lfloor x/2^k \rfloor$ towards negative infinity)

Floating Point Representation

Definition

$(-1)^s\times(1+Significand)\times2^{E-bias}$

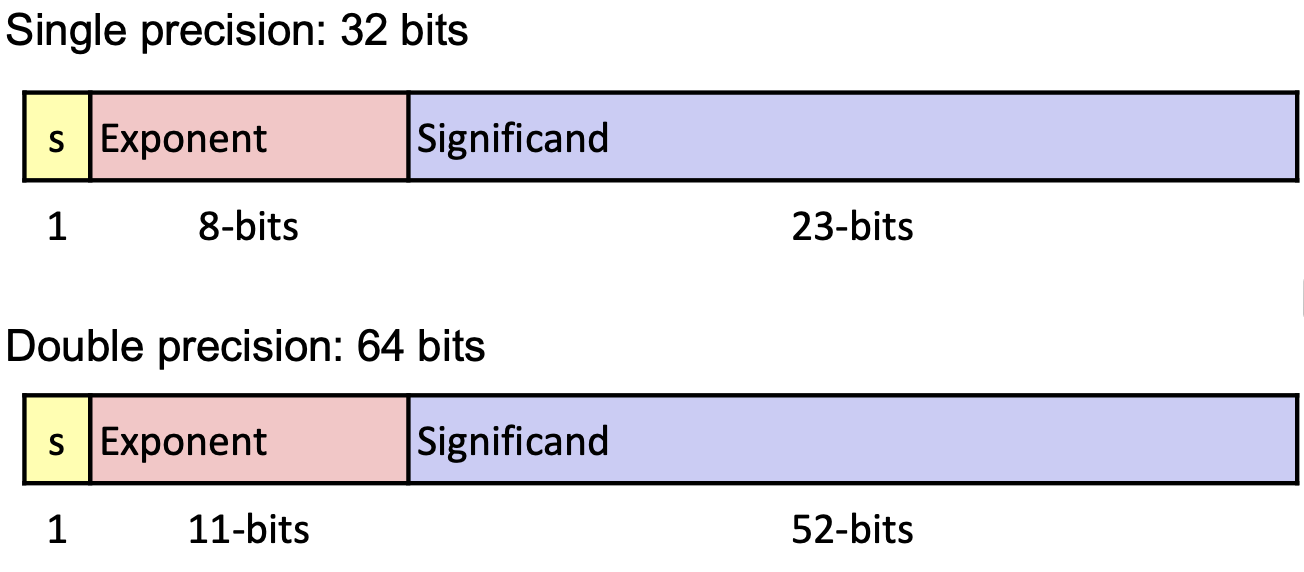
• S represents Sign

  1 for negative, 0 for positive

• Significand

  implicit leading 1, signed-magnitude (not 2’s complement)

• Exponent(biased notation)

  Idea: we want floating point numbers to look small when their actual value is small

  $-(2^{k-1}-1)\rightarrow2^k$(bias of 127 for 32bits, 1023 for 64bits)

Special Cases

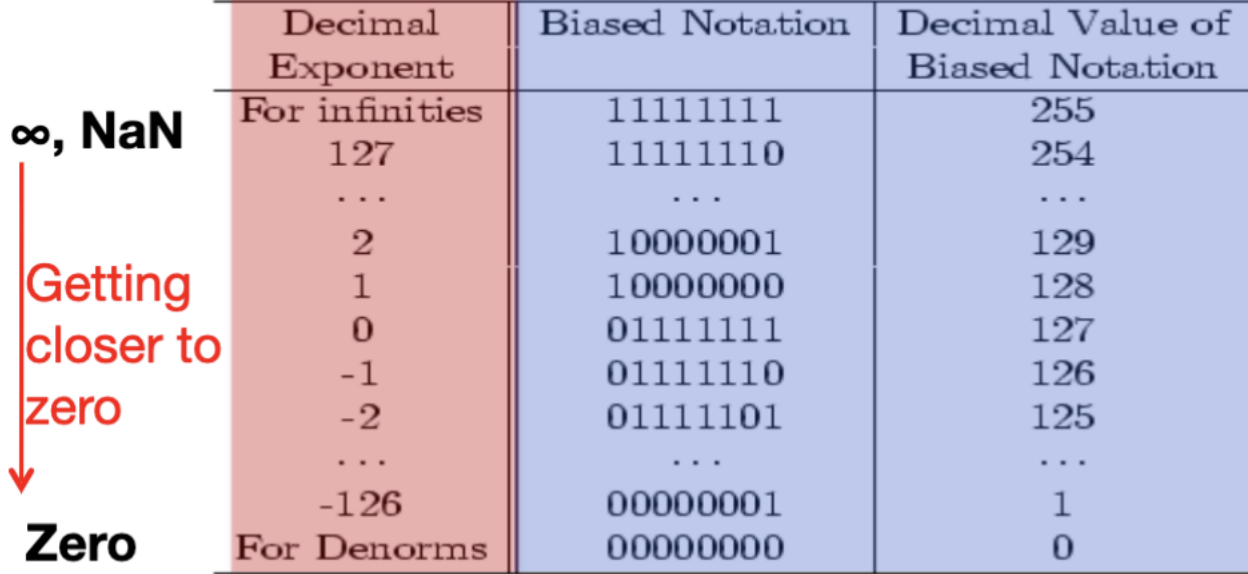
Exponent(Biased)	Significand	Object
0	0	$\pm0$
0	nonzero	Denorm
1-254	aynthing	Normal Floating Point
255	0	$\pm\infty$
255	Nonzero	NaN

Overflow and Underflow

• Overflow ($>2^{128}$or$<-2^{128}$)
• Underflow ($-2^{149}<x<2^{149}$ without 0)

0,infinite and NAN

• 0:Bit pattern all 0s
• $\infty$($1\div0$)
  • Sign bit 0 or 1, largest exponent (all 1s), 0 in fraction
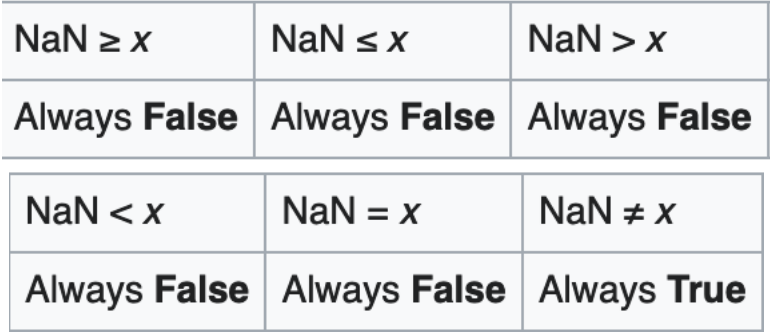
• NaN($\infty-\infty$,$0\div0,\sqrt{-4}$)
  • Sign bit 0 or 1, largest exponent (all 1s), not zero in fraction

op(NaN, X) = NaN

Demorms

Denormalized number:

• no (implied) leading 1(just Significand),frac nonzero
• exponent all 0,value = 1 – Bias (instead of 0 – Bias)

Special Cases:

• Smallest denorm: $\pm0.0...01\times2^{-126} = \pm2^{-149}$
• Largest denorm: $\pm0.1...1\times2^{-126} = \pm2(^{-126}-2^{-149})$
• Smallest norm: $\pm1.0...0\times2^{-126}=\pm 2^{-126}$
• Largest norm: $\pm1.1...1\times2^{127}=\pm (2^{128}-2^{104})$