3 Data Structure

Big O Notation

• $f(n) = O(g(n))$
  • $\exist k>0,n_0,\forall n>n_0, f(n)\leq kg(n)$
• $f(n) = \Omega(g(n))$
  • $\exist k>0,n_0,\forall n>n_0, f(n)\geq kg(n)$
• $f(n) = \Theta(g(n))$
  • $\exist k_1>0, k_2>0,n_0,\forall n>n_0, k_1g(n)\leq f(n)\leq k_2g(n)$

Substution Method

• Base case: show that the statement is true for the smallest value of 𝑛 (typically 0)
• Induction step: assuming that the statement is true for any $k < n$, show that it must also hold for $n$

Master Method

$$T(n) = \begin{cases} d & n \leq n_0 \\ aT(\frac nb) + f(n) & otherwise \end{cases}$$

Compare which part is bigger

• case1: for some $\epsilon > 0$, $f(n) = O(n^{\log_b^a - \epsilon}) \Rightarrow T(n) = \Theta(n^{\log_b^a})$

• case2: $f(n) = \Theta(n^{\log_b^a}) \Rightarrow T(n) = \Theta(n^{\log_b^a}\log n)$

  for some $k\geq 0$, $f(n) = \Theta(n^{\log_b^a}(\log n)^k)\Rightarrow T(n) = \Theta(n^{\log_b^a}(\log n)^{k+1})$

• case3: for some $\epsilon > 0$, $f(n) = \Omega(n^{\log_b^a} + \epsilon)$ and $\exist c < 1, \forall n > n_0, af(\frac nb) \leq cf(n)$ $\Rightarrow T(n) = \Theta (f(n))$

P and NP

Problems, Instances and Algorithms:

• Problem: Max-Flow
• Instance: A graph G with edge-capacities, two vertices s, t, and an integer k
• Algorithm: It takes as input an instance, and outputs either 'YES' or 'NO'

Reductions:

• A $\leq$ B: A reduces to B if an instance $I_A$ is YES iff $I_B$ is YES
• A $\leq_p$ B: A is polynomial time reducible to B. There is an algorithm A that has the following properties:
  • given an instance $I_X$ of X, A produces an instance $I_Y$
  • A runs in time $O(|I_X|^k)$.
  • Answer to $I_X$ is YES iff answer to $I_Y$ is YES.
• Theorem1: If A $\leq_p$ B and B $\in$ P, then A $\in$ P
• Theorem2: If A $\leq_p$ B and B $\leq_p$ C, then A $\leq_p$ C (transitivity)

P and NP:

• P(Polynomial): The set of all decision problems that have an algorithm that runs intime $O(n^k)$ for some constant $k$
• NP(nondeterministic polynomial): NP is the set of existential questions that can be verified in polynomial time
• NP hard: B is NP hard if A $\leq_p$ B for all A $\in$ NP
• NP complete
  • Definition: B in NP and B is NP hard
  • Theorem: If B $\leq_p$ C, C $\in$ NP, and B is NP complete, then C is NP complete(Proof using transitivity)

Typical NP complete problem

• SAT
• 3-SAT
• Clique
• Independent Set
• vertex cover
• Hamiltonian Cycle

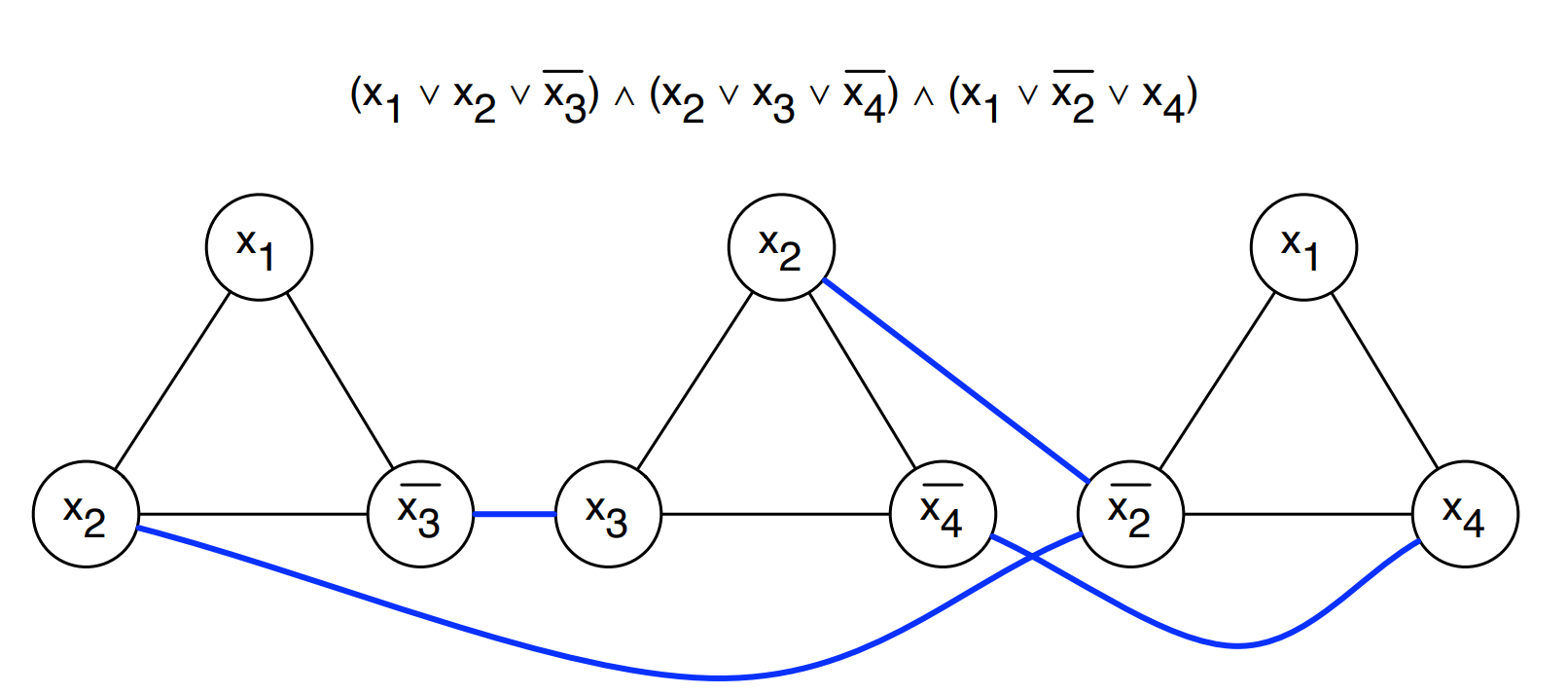
3SAT $\leq_p$ Independent Set

• If the formula is satisfiable, there is at least one true literal in each clause. Let S be a set of one such true literal from each clause. |S| = k and no two nodes in S are connected by an edge.
• If the graph has an independent set S of size k, we know that it has one node from each “clause triangle.” Set those terms to true. This is possible because no 2 are negations of each other.

DNF(disjunctive normal form)

CNF(conjunctive normal form)

Hashmap

Implement	contains(x)	add(x)
Bushy BSTs	Θ(log N)	Θ(log N)
Separate Chaining Hash Table With No Resizing	Θ(N)	Θ(N)
… With Resizing	Θ(1)	Θ(1)

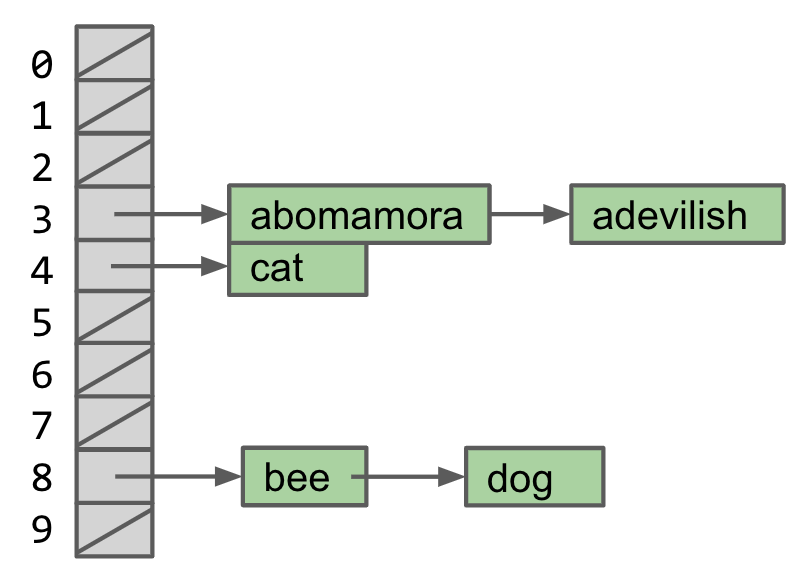
Separate Chaining Data Indexed Array

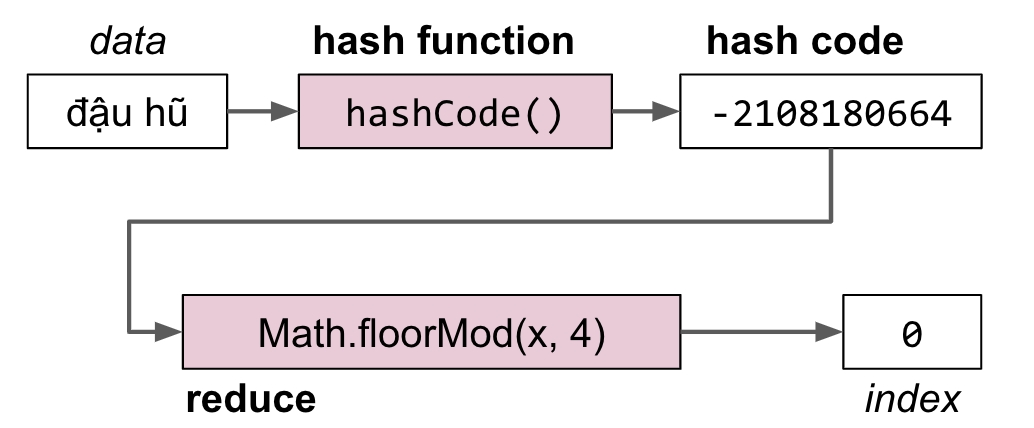
Data is converted into a hash code. The hash code is then reduced to a valid index.

Java’s hashCode() function for Strings

public int hashCode() {// From Left to right: High to Low
    int h = cachedHashValue;
    if (h == 0 && this.length() > 0) {
        for (int i = 0; i < this.length(); i++) {
            h = 31 * h + this.charAt(i);
        }
        cachedHashValue = h;
    }
    return h;
}

31: the hashCode base should be a small prime to avoid overflow

suppose the number of buckets: M, number of items: N

then complexities of contains and add are O(Q = N/M)

To make them O(1), strategy: When N/M is ≥ 1.5, double M

bool contains(int x, vector<list<int>>& hash_table){
    int n = hash_table.size();
    int index = (x%n + n)%n;
    list<int>& slot = hash_table[index]; 
    return find(slot.begin(),slot.end(),x)!=slot.end();
}
bool add(int x,vector<list<int>>& hash_table){
    int n = hash_table.size();
    int index = (x%n + n)%n;
    hash_table[index].push_back(x);
}

Open Addressing

An alternate way to handle collisions is to use open addressing

If target bucket is already occupied, use a different bucket

• Linear probing
  • Use next address, and if already occupied, just keep scanning one by one.
• Quadratic probing
  • Use next address, and if already occupied, try looking 4 ahead, then 9 ahead, then 16 ahead, ...

Sort

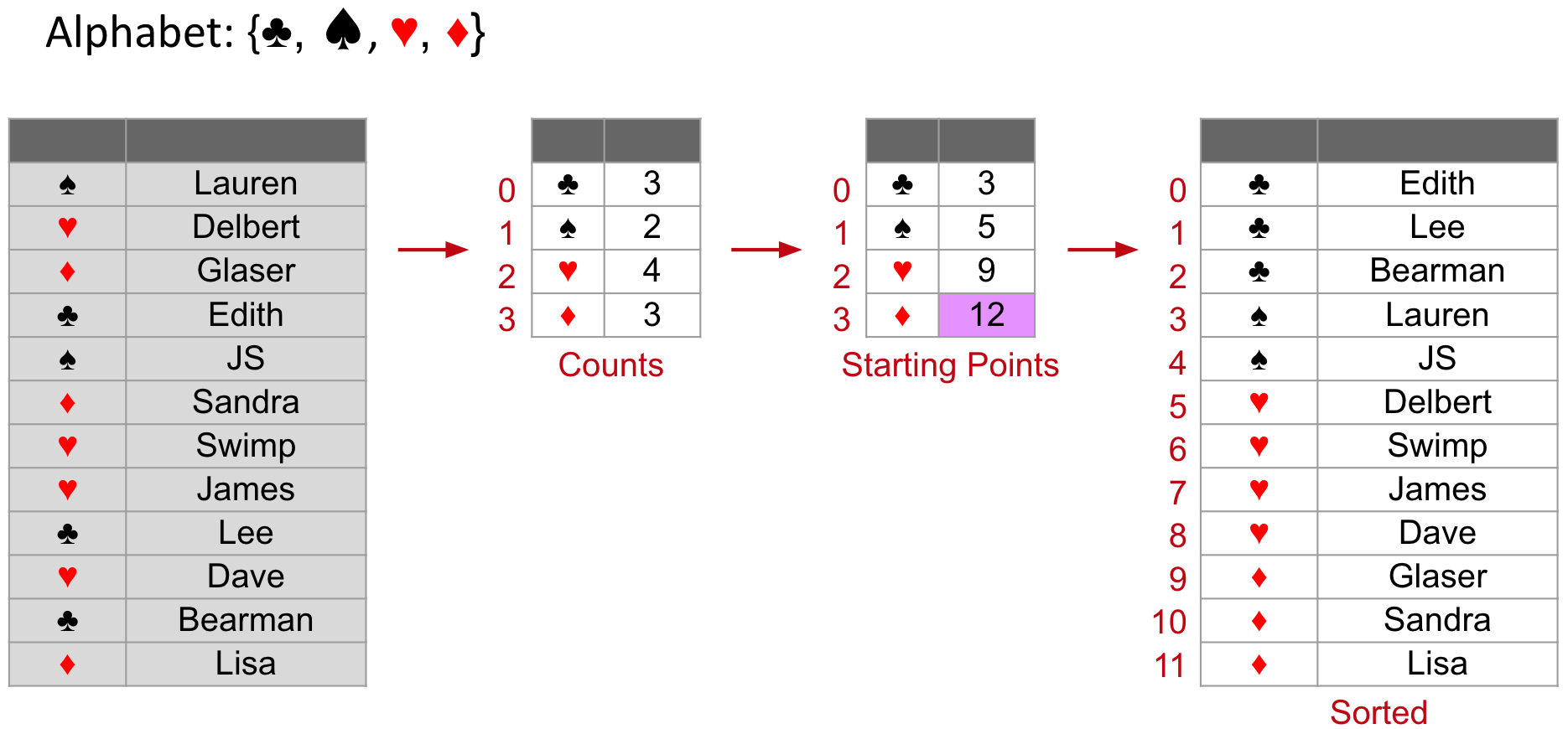
Counting Sort

Procedure:

• Find the range
• Count number of occurrences of each item
• Iterate through list, using count array to decide where to put everything

If the size of the hashmap is R, then

• Runtime: Θ(N+R)
• Memory: Θ(N+R)(Result Θ(N))

Radix Sort

LSD Radix Sort

Sort each digit independently from rightmost digit towards left

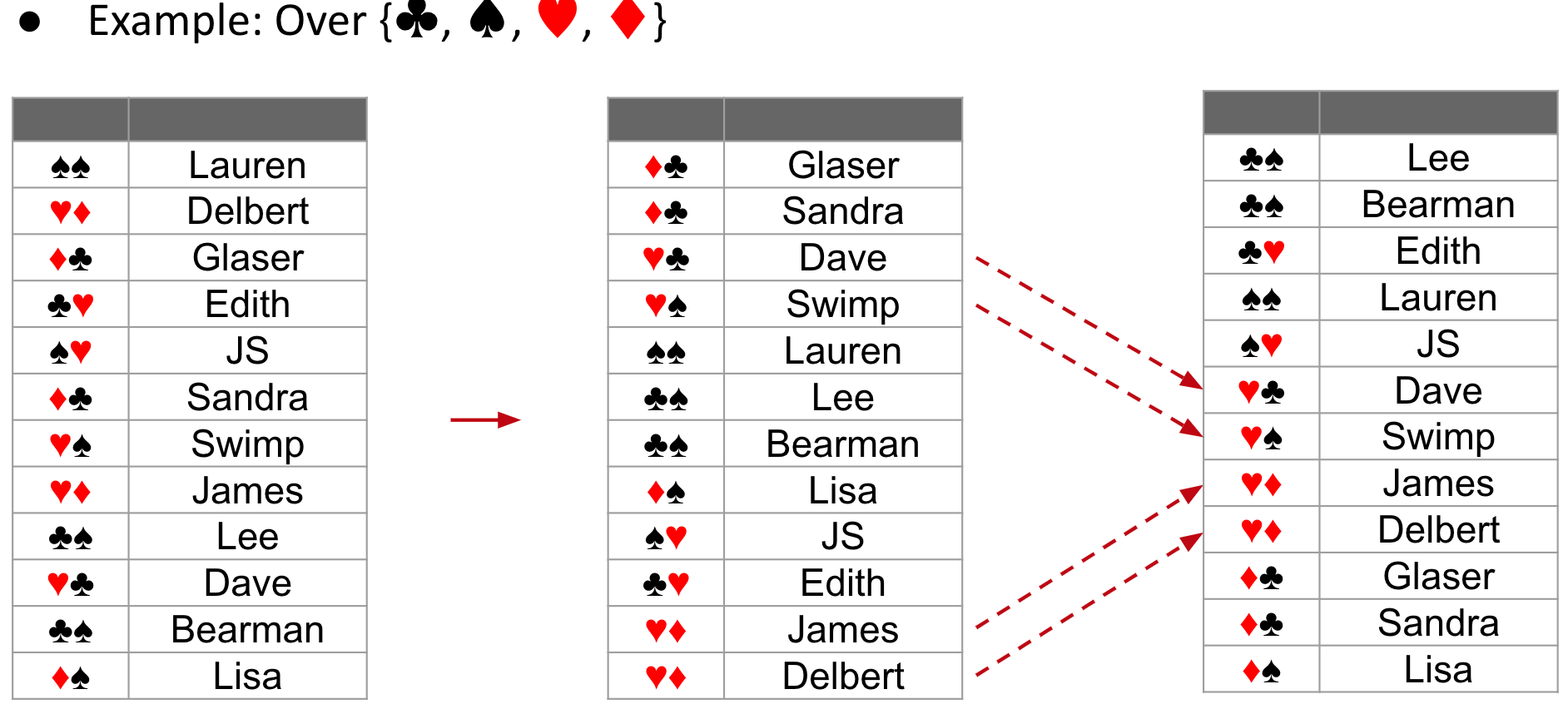
W: Width of each item in # digits

Runtime: Θ(WN+WR)

MSD Radix Sort

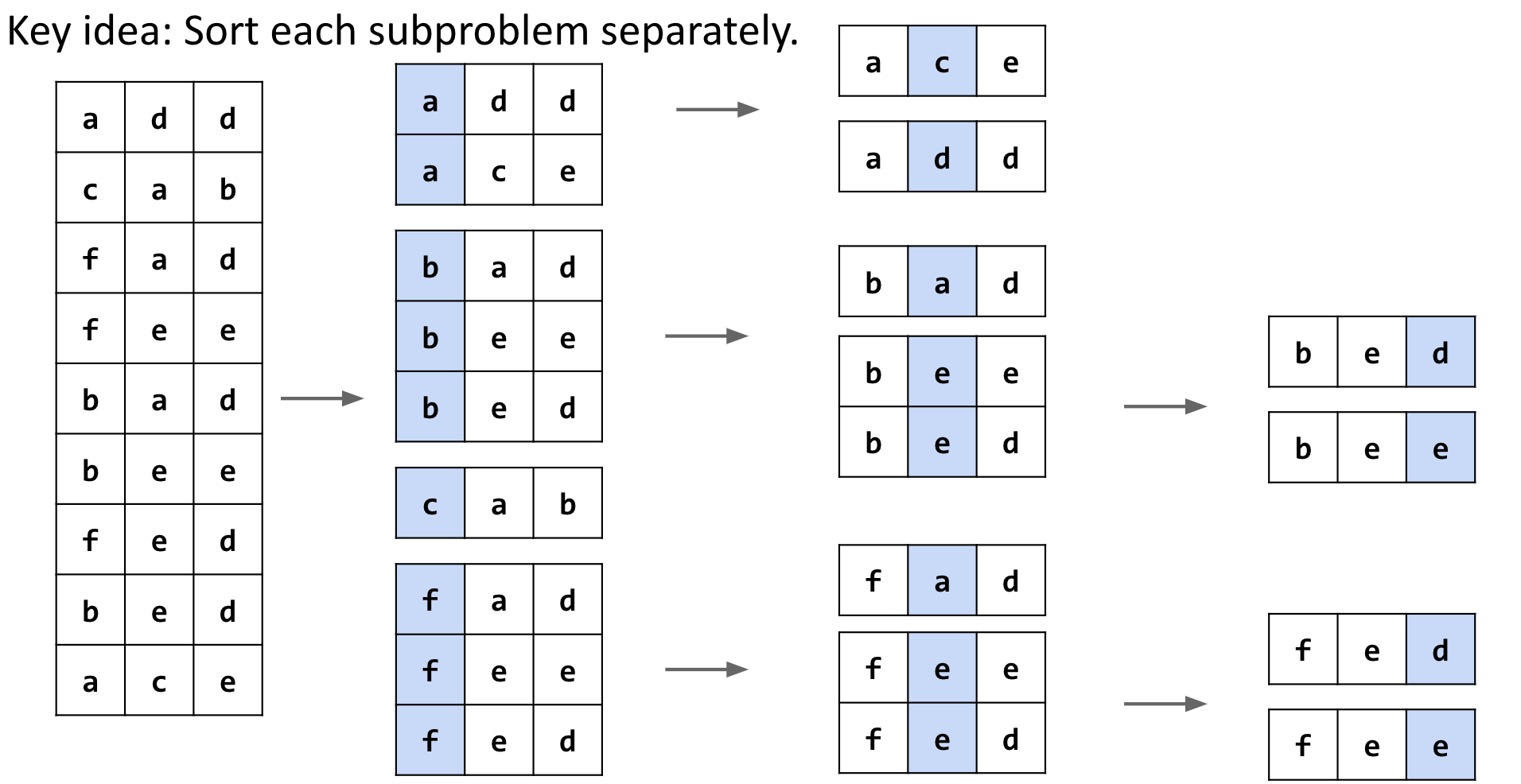
• Best Case: finish in one counting sort pass, looking only at the top digit: Θ(N + R)
• Worst Case: look at every character, degenerating to LSD sort: Θ(WN + WR)

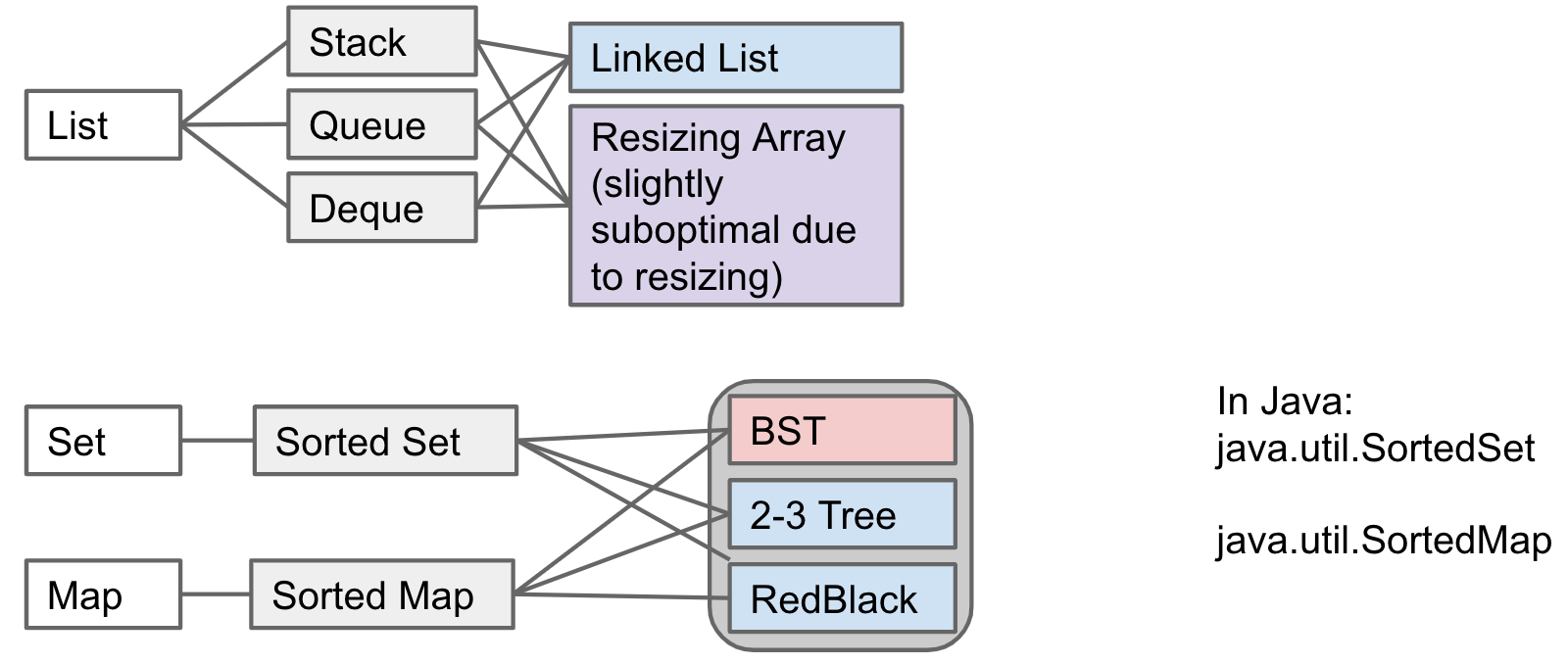
List,Set,Map

Heap

Binary heap: Binary tree that is complete and obeys heap property

• Min-heap: Every node is less than or equal to both of its children
• Max-heap: Every node is greater than or equal to both of its children

Priority Queue Implementation

Implement	Ordered Array	Bushy BST	Hash Table	Heap
add	Θ(N)	Θ(log N)	Θ(1)	Θ(log N)
getSmallest	Θ(1)	Θ(log N)	Θ(N)	Θ(1)
removeSmallest	Θ(N)	Θ(log N)	Θ(N)	Θ(log N)

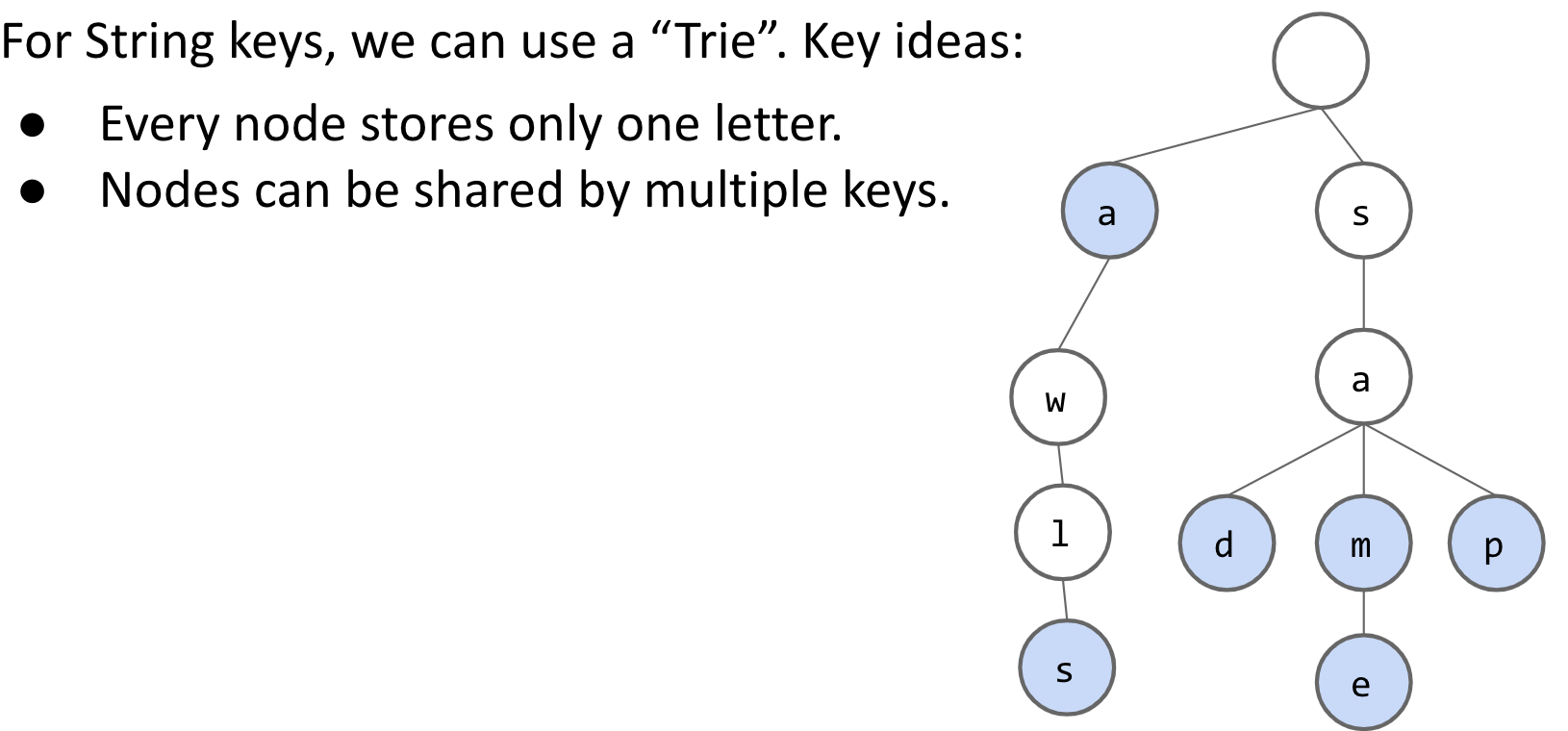
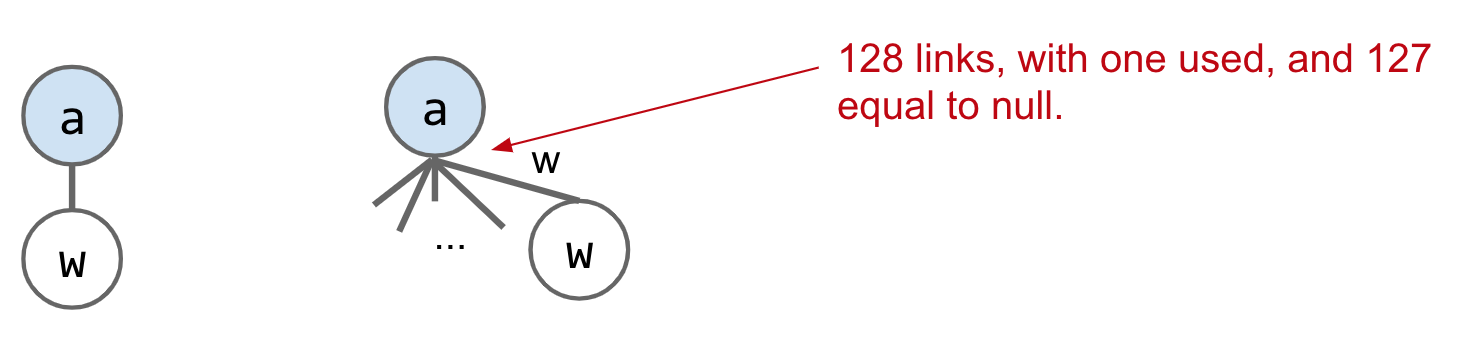
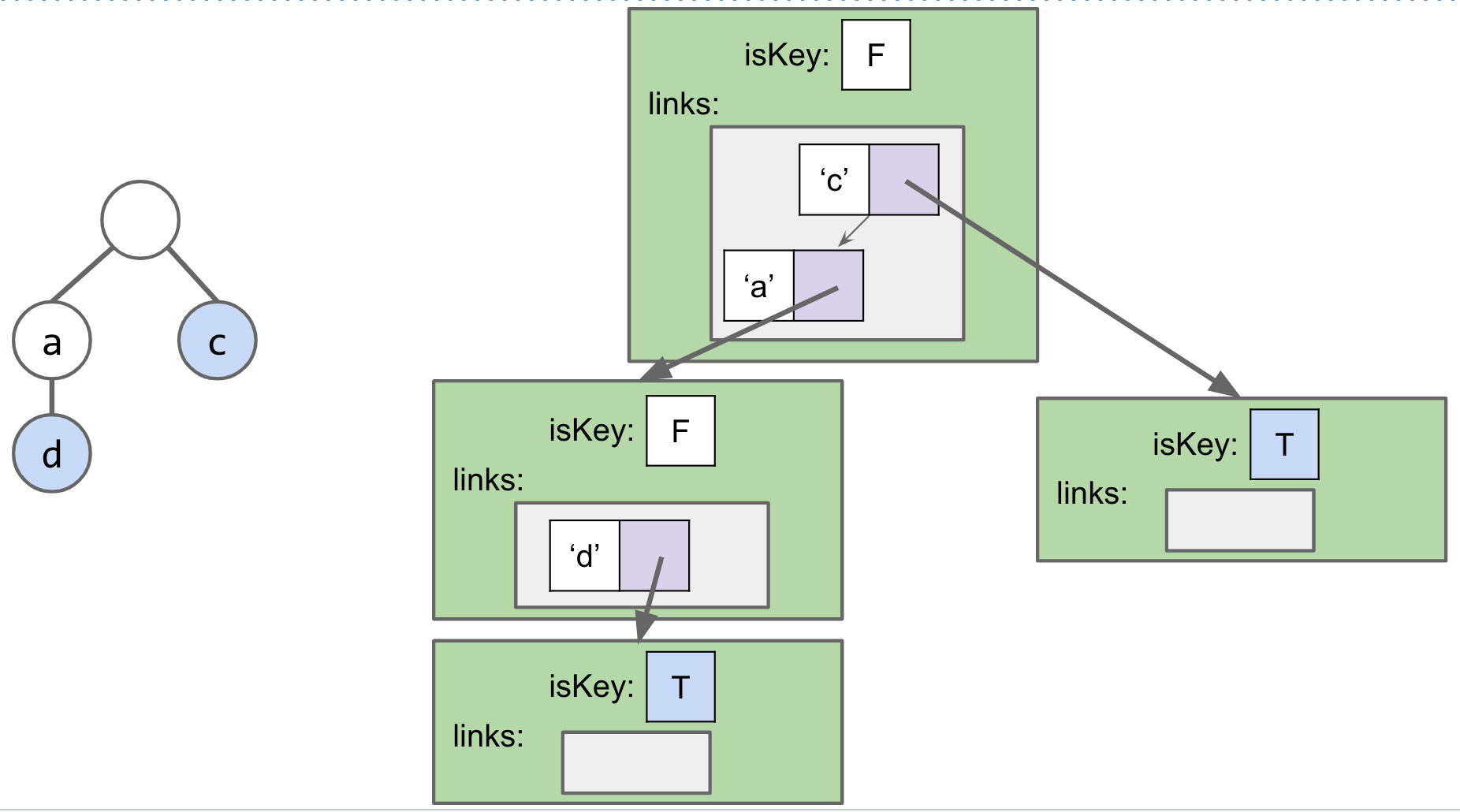
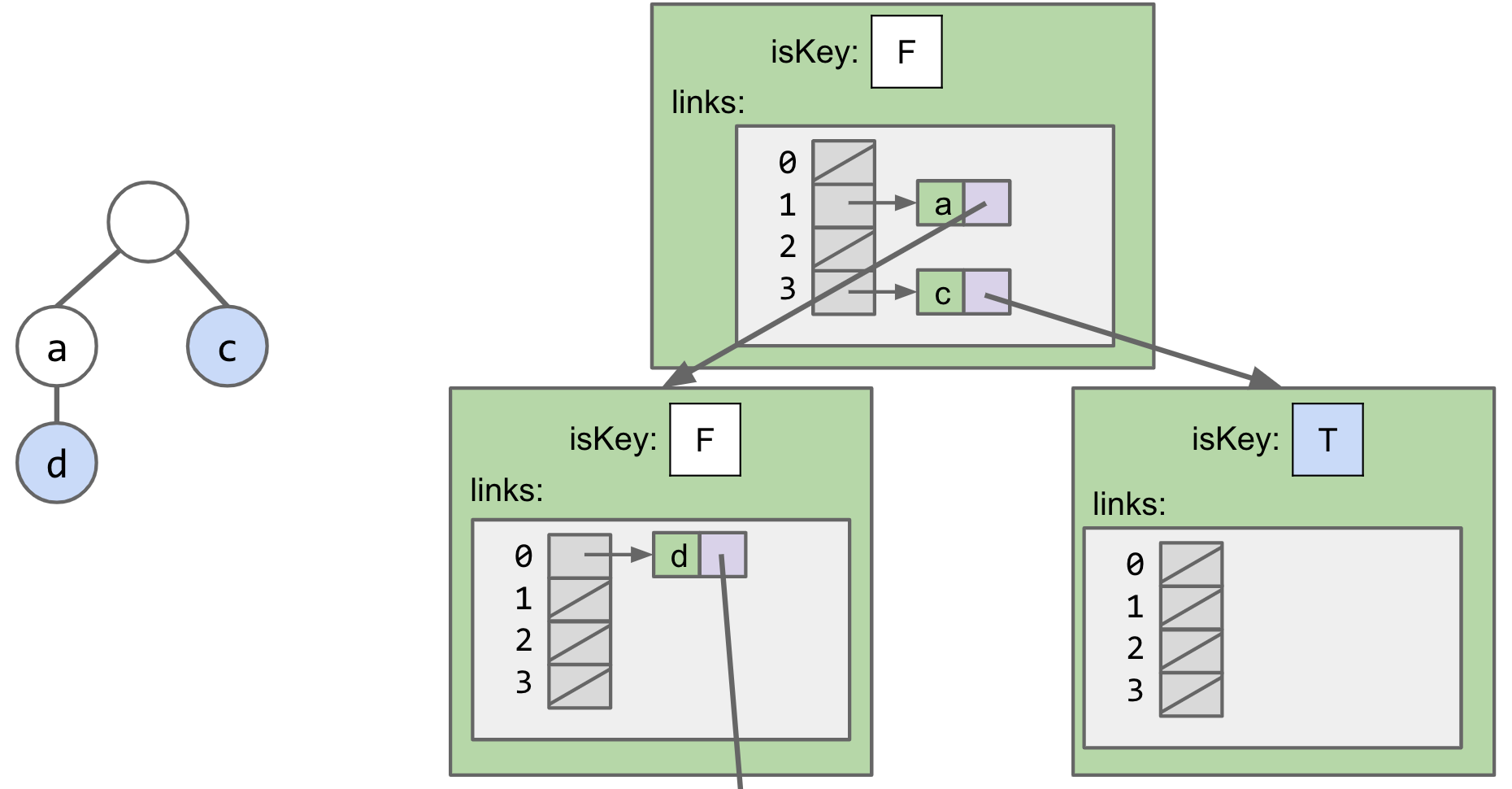
Trie

Each Node Stores One Character, keys in blue

Implementation

DataIndexedCharMap

BST

Separate Chaining Hash Table

Analysis

Contains and Add in O(L)(the length of the key), for each node:

• DataIndexedCharMap is Θ(1).
• BST is O(log R), where R is size of alphabet.
• Hash Table is O(R), where R is size of alphabet.

Space:

• DataIndexedCharMap: 128 links per node.
• BST: C links per node, where C is the number of children.
• Separate Chaining Hash Table: C links per node.