5 Parallelism

Basics

Amdahl’s Law

Speedup =$\frac{t_{prev}}{t_{cur}} = \frac{1}{(1-F)+F/S}$

F = Fraction of execution time speed up

S = Scale of improvement

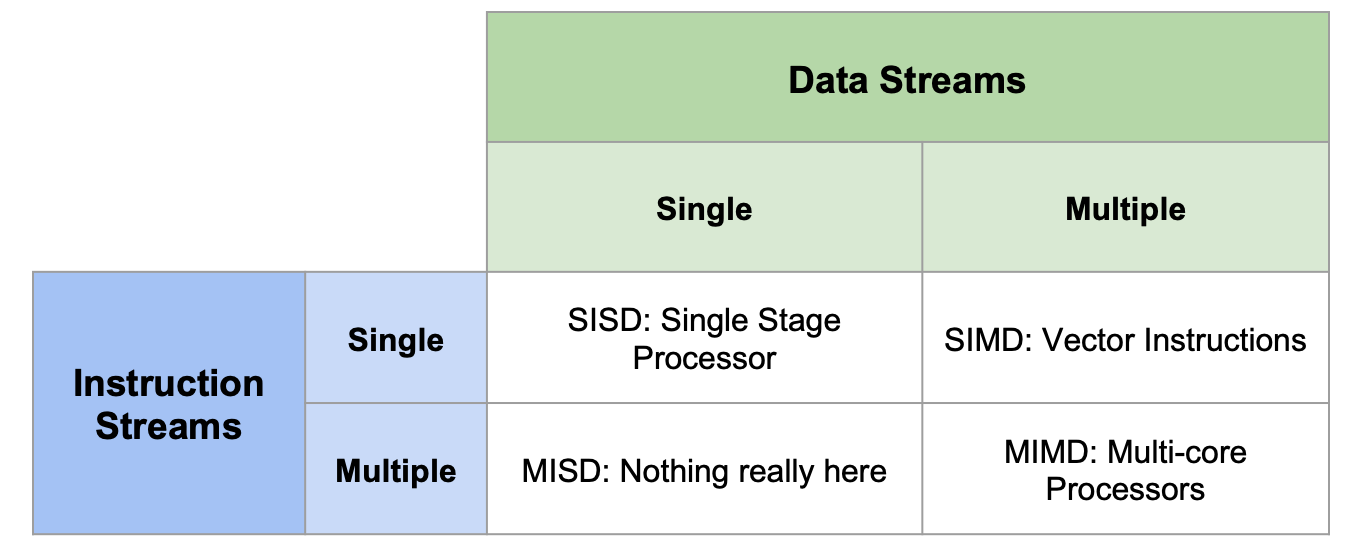
SIMD

SIMD Architecture

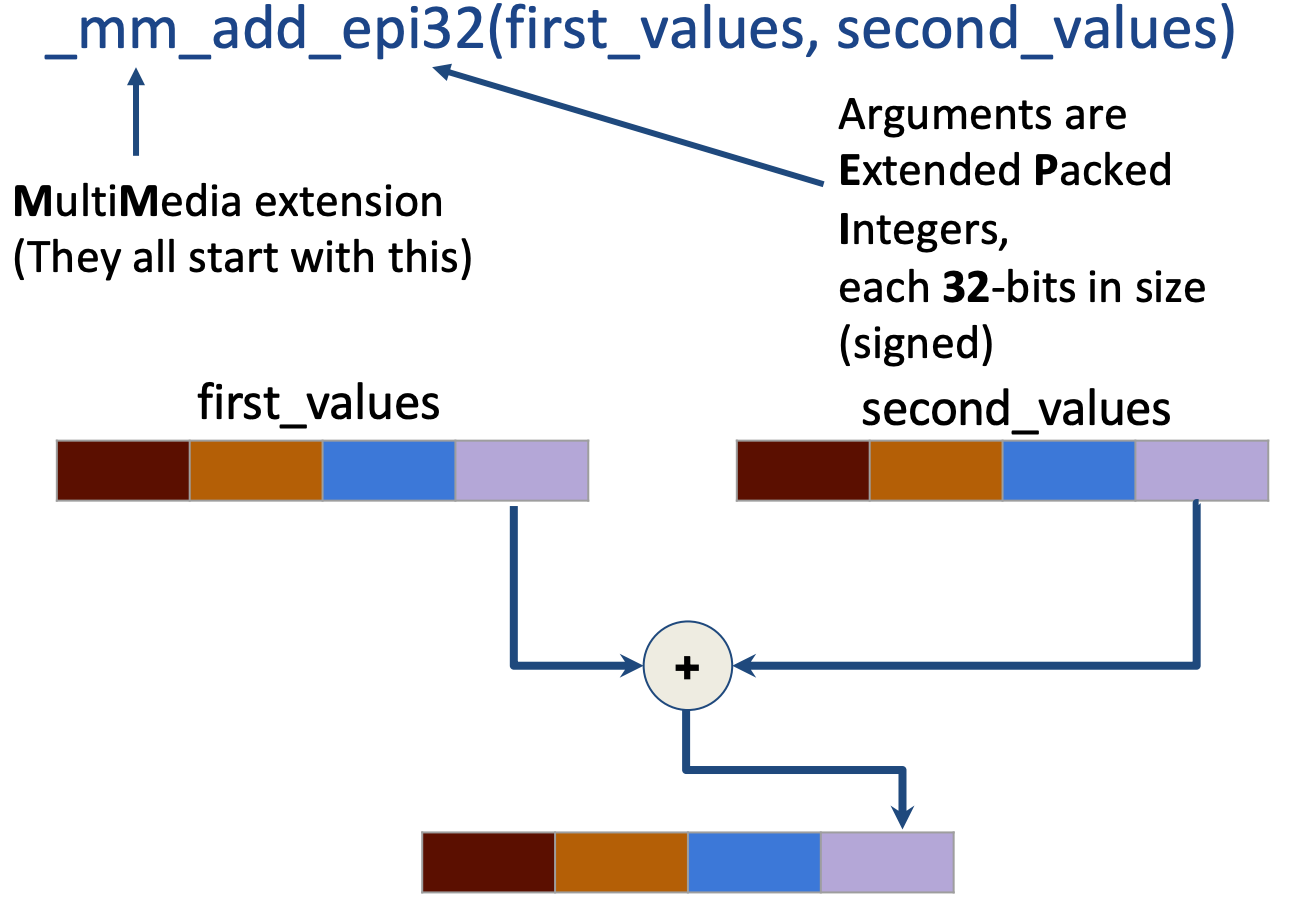
X86 Intrinsics AVX Data Type

Intrinsics AVX Code nomenclature [ˈnomənˌkletʃɚ]name call

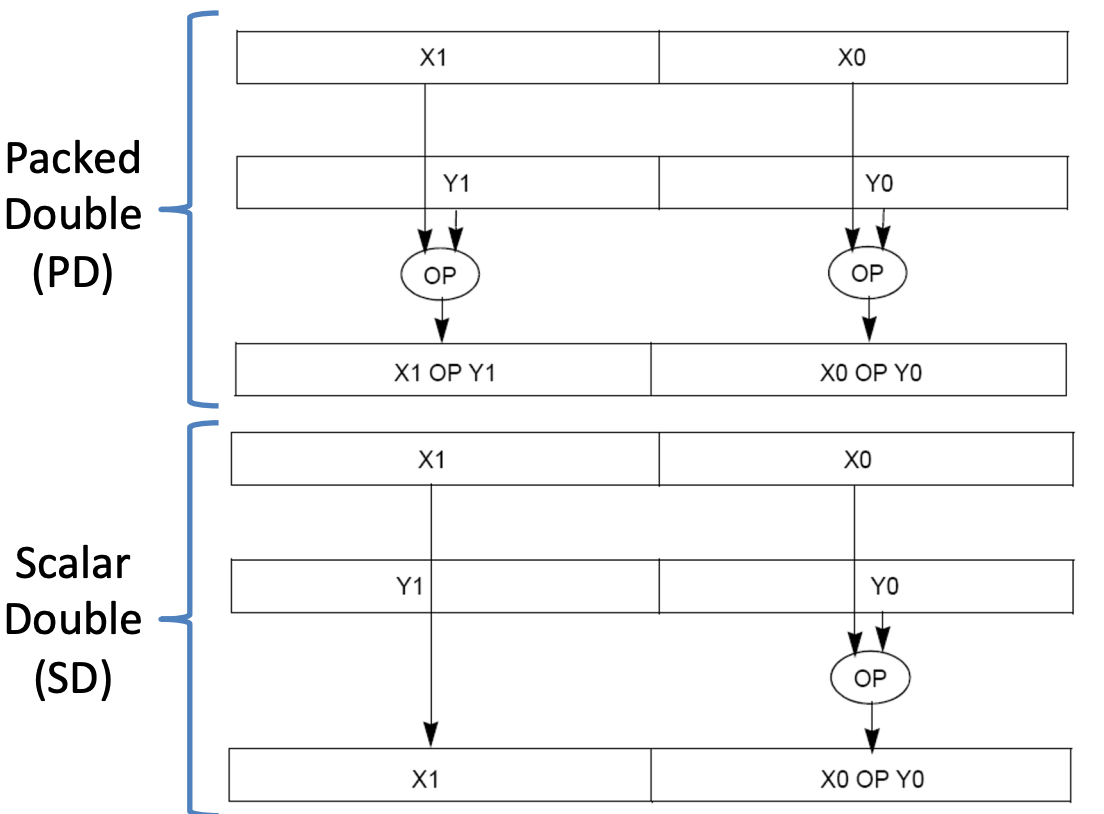
Example

Loop Unrolling

Loop Unrolling in C

for(i=0; i<1000; i++)
    x[i] = x[i] + s;
//Unrolling
for(i=0; i<1000; i=i+4) {
    x[i] = x[i] + s;
    x[i+1] = x[i+1] + s;
    x[i+2] = x[i+2] + s;
    x[i+3] = x[i+3] + s;
}

RISCV

Loop:
lw t0, 0(s0)
addu t0,t0,s1 # add b to array element
sw t0,0(s0) # store result
addi s0,s0,4 # move to next element
bne s0,s2,Loop # repeat Loop if not done

Unrolling Loop:
lw t0,0(s0)
lw t1,4(s0)
lw t2,8(s0)
lw t3,12(s0) # 4 wide SIMD Load
add t0,t0,s1
add t1,t1,s1
add t2,t2,s1
add t3,t3,s1 # 4 wide SIMD Add
sw t0,0(s0)
sw t1,4(s0)
sw t2,8(s0)
sw t3,12(s0) # 4 wide SIMD Store
addi s0,s0,16
bne s0,s2,Loop

Matrix Multiply

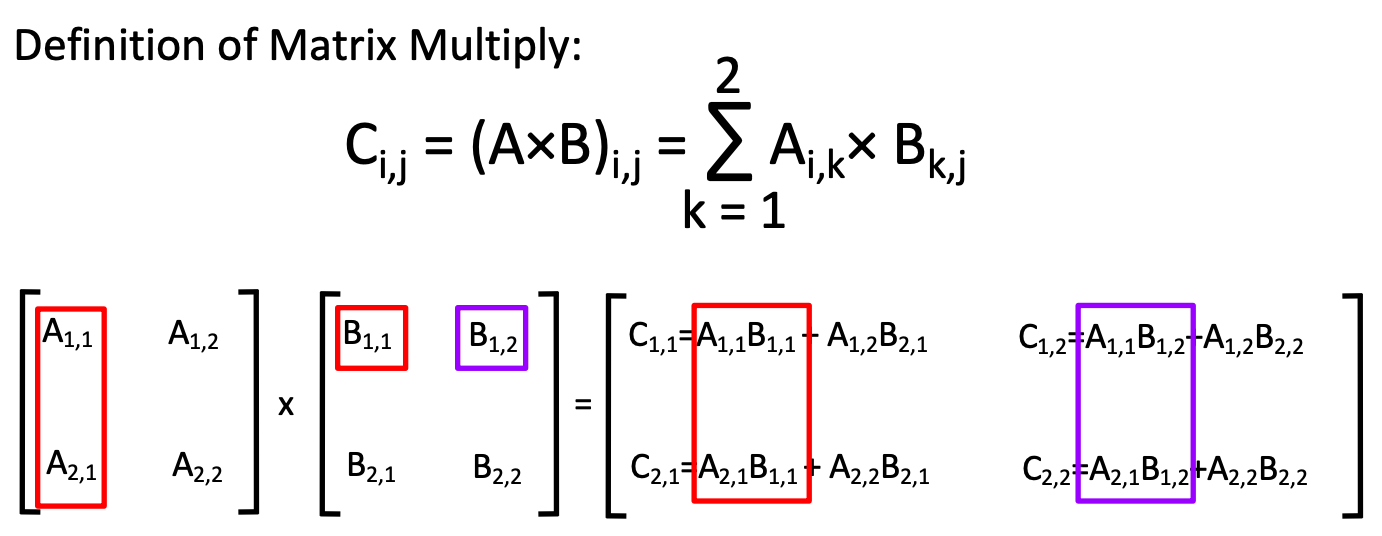
Now, i、j、k are N, we divide i by 4 each block.

so C[i][j] whole row can be divided by 4, each column entry(j) can be divided by N(k)

#include <x86intrin.h>
void mm_scalar(int N, double *a, double *b, double *c) {
    for(int i=0;i<N;i+=4){
        for(int j=0;j<N;++j){
            __m256d c0 = {0,0,0,0};
            for (k = 0; k < N; k++) {
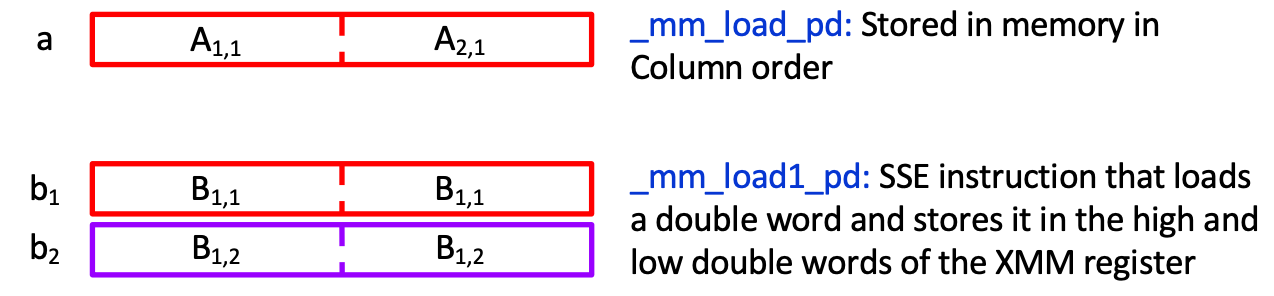
                c0 = _mm_add_pd(c0,_mm_mul_pd(_mm_load_pd(a+i+k*N),_mm_load1_pd(b+k+j*N)))
                //c0 += a[i][k] * b[k][j]
            }
            _mm_store_pd(c+i+j*N,c0);
        }
    }
    return 0;
}
const int UNROLL = 4;
// Unrolling
void mm_unroll(int N, double *A, double *B, double *C) {
    for (int i=0;  i<n;  i+= UNROLL*4) {
        for (int j=0;  j<n;  j++) {
            __m256d c[4];
            for (int x=0;  x<UNROLL;  x++)
                c[x] = _mm_load_pd(C+i+x*4+j*N);
            for (int k=0;  k<n;  k++) {
                __m256d b = _mm_load1_pd(B+k+j*n);
                for (int x=0;  x<UNROLL;  x++)
                    c[x] = _mm_add_pd(c[x],
                           _mm_mul_pd(_mm_load_pd(A+i+x*4+k*N), b));
            }
            for (int x=0;  x<UNROLL;  x++) 
                _mm_store_pd(C+i+x*4+j*N, c[x]);     
        }
    }
}
// Cache Blocking
const int BLOCKSIZE = 32;

void do_block(int n, int si, int sj, int sk, double *A, double *B, double *C) {
    for (int i=si;  i<si+BLOCKSIZE;  i+=UNROLL*4)
        for (int j=sj;  j<sj+BLOCKSIZE;  j++) {
            __m256d c[4];
            for (int x=0;  x<UNROLL;  x++)
                c[x] = _mm_load_pd(C+i+x*4+j*N);
            for (int k=sk;  k<sk+BLOCKSIZE;  k++) {
                __m256d b = _mm_load1_pd(B+k+j*n);
                for (int x=0;  x<UNROLL;  x++)
                    c[x] = _mm_add_pd(c[x],
                           _mm_mul_pd(_mm_load_pd(A+i+x*4+k*N), b));
            }
            for (int x=0;  x<UNROLL;  x++) 
                _mm_store_pd(C+i+x*4+j*N, c[x]); 
        }
}

void mm_block(int n, double* A, double* B, double* C) {
    for(int sj=0;  sj<n;  sj+=BLOCKSIZE) 
        for(int si=0;  si<n;  si+=BLOCKSIZE)
            for (int sk=0;  sk<n;  sk += BLOCKSIZE)
                do_block(n, si, sj, sk, A, B, C);
}

MIMD

OpenMP

Synchronization

Reduction: specifies that 1 or more variables that are private to each thread are subject of reduction operation at end of parallel region

double compute_sum(double *a, int a_len) {
    double sum = 0.0;
    #pragma omp parallel for reduction(+ : sum)
    for (int i = 0; i < a_len; i++) {
        sum += a[i];
    }
    return sum;
}

Pitfalls

• Data dependencies

  a[0] = 1;
  for(i=1; i<5000; i++)
      a[i] = i + a[i-1];

• Sharing Issues

  // Problem
  #pragma omp parallel for //Each thread accesses different elements of a, b,and c, but the same temp
  for(i=0; i<n; i++){
      temp = 2.0*a[i];
      a[i] = temp;
      b[i] = c[i]/temp;
  } 
  // Correct
  #pragma omp parallel for private(temp)
  for(i=0; i<n; i++){
      temp = 2.0*a[i];
      a[i] = temp;
      b[i] = c[i]/temp;
  }

• Updating Shared Variables Simultaneously

  This can be done by surrounding the summation by a critical/atomic section or reduction clause

• Parallel Overhead

  Parallelize over the largest loop that you can (even though it will involve more work to declare all of the private variables and eliminate dependencies)