4 Cache

Basic

Principle of Locality

• Temporal Locality (locality in time)

  If a memory location is referenced then it will tend to be referenced again soon

• Spatial Locality (locality in space)

  If a memory location is referenced, the locations with nearby addresses will tend to be referenced soon

Caching Terminology

• Cache hit

  Cache holds a valid copy of the block, so return the desired data

• Cache miss

  Cache does not have desired block, so fetch from memory and put in empty (invalid) slot

Average Memory Access Time(AMAT) = Hit time + Miss rate × Miss penalty

Cache block replacement policy

• Random Replacement

• Least Recently Used (LRU)

  Replace block we used(hit & miss) least recently first in the hopes we will use it again later than all other blocks

• FIFO

  Replace block we miss least recently

Caching Read & Write

we assume the use of separate instruction and data caches (Icache and Dcache)

• Read from both
• Write only to Dcache (assume no self-modifying code)

Write Hits

• Write-Through Policy: Always write data to cache and to memory (through cache)
• Write-Back Policy: Write data only to cache, then update memory when block is removed
  • Dirty bit Extra bit per cache row that is set if block was written to (is "dirty") and needs to be written back

Write Miss

• Write Allocate policy: when we bring the block into the cache after a write miss

  • Write allocate almost always paired with write-back(Memory is always up-to-date)

• No Write Allocate policy: only change main memory after a write miss

  • No write allocate typically paired with write-through(Cache is always up-to-date)

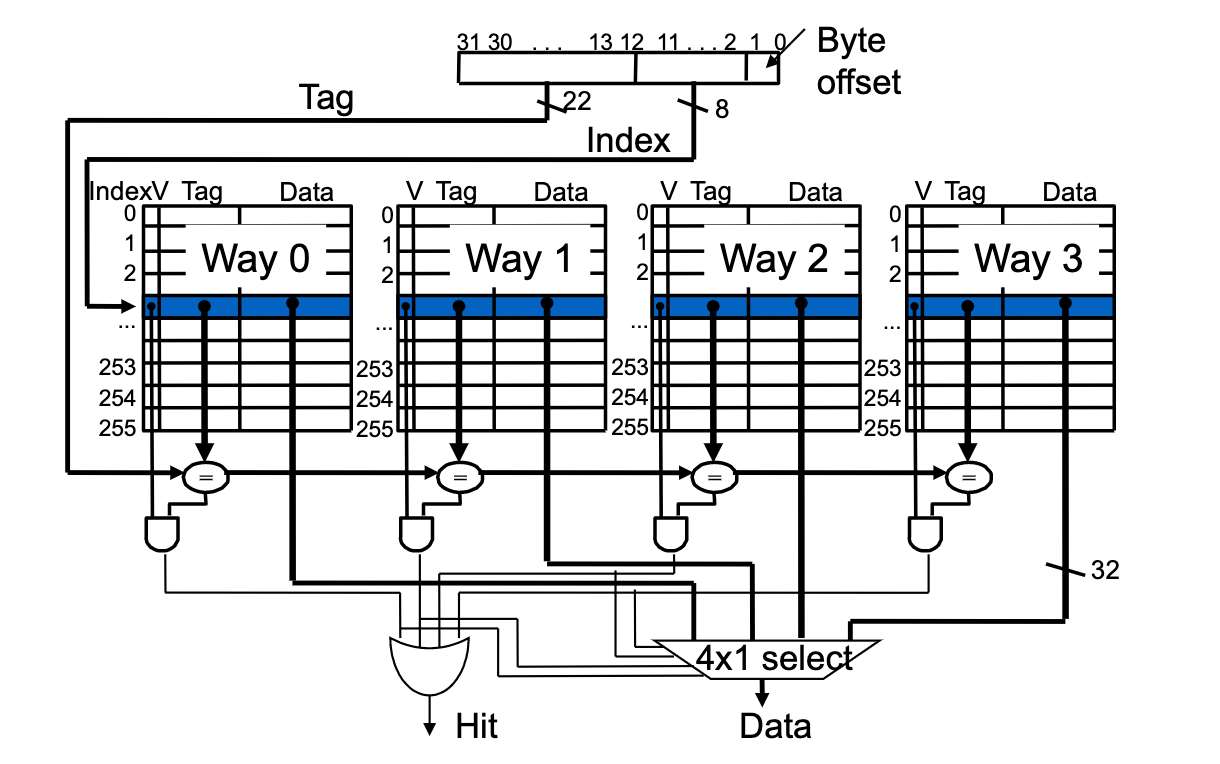
Processor Address Fields

a cache of fixed size (C), Memory is (A) byte-addressed

• Offset: denotes block size: (# = K) Bytes

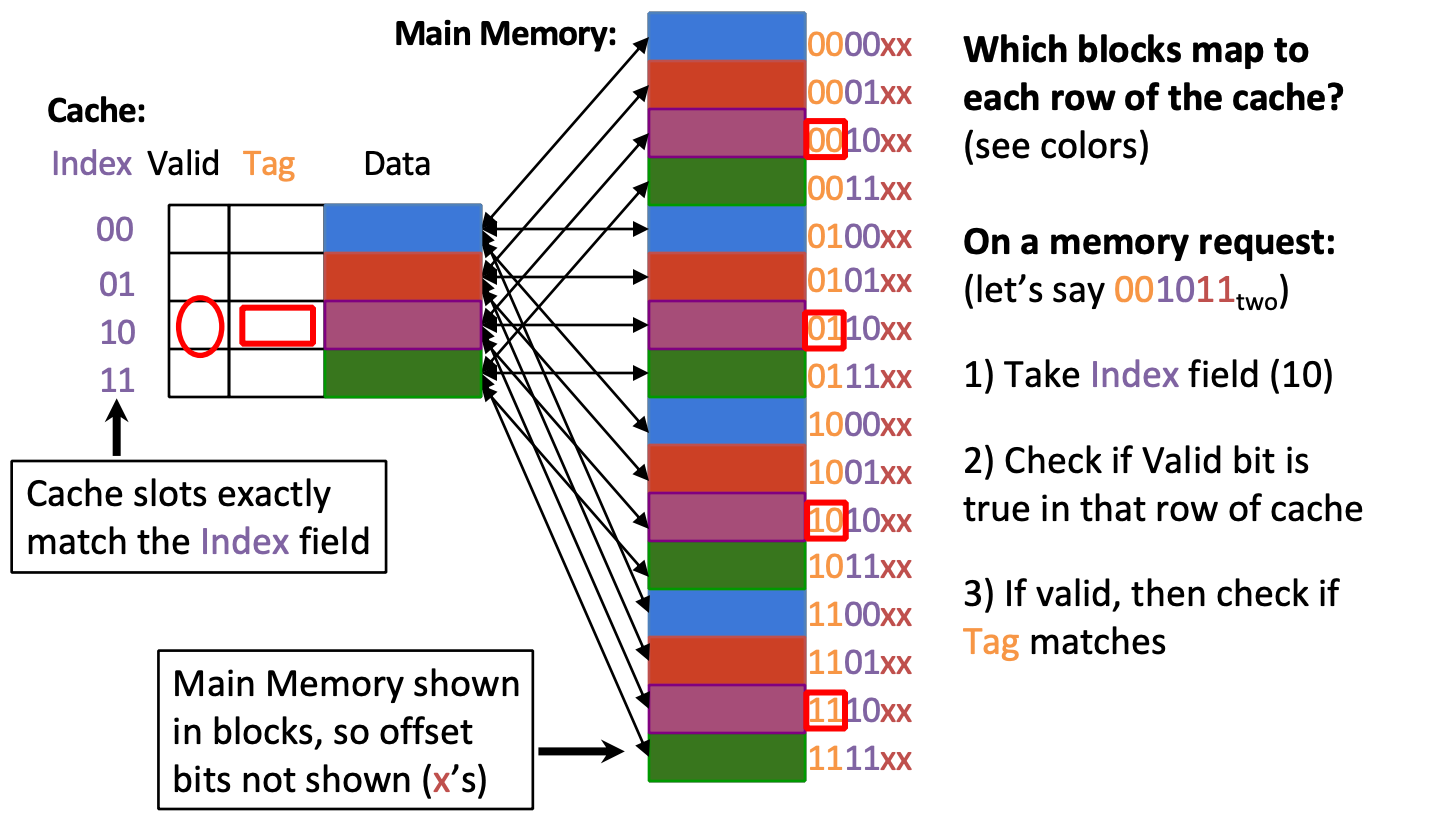
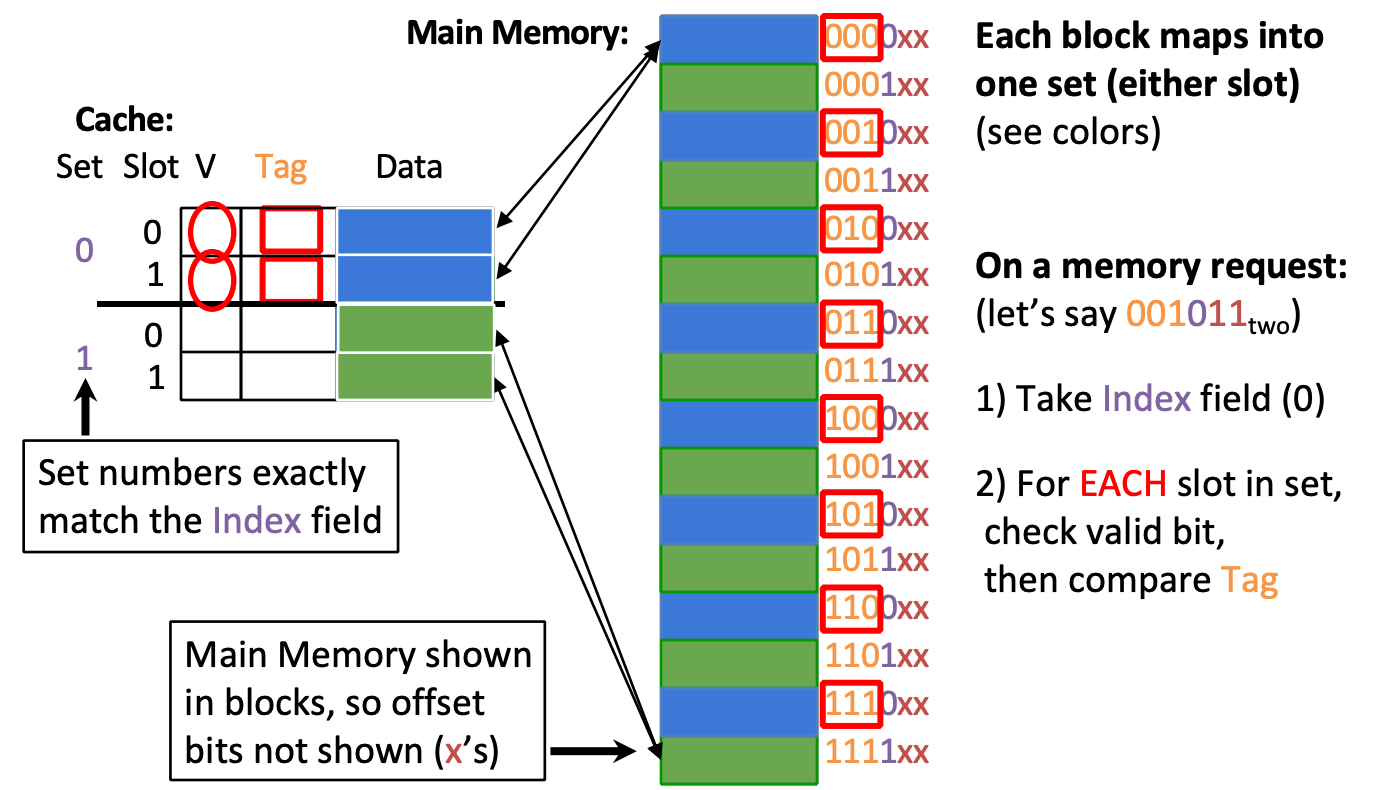
• Index: Can’t fit all blocks at once, multiple blocks in memory must map to the same “set” in cache

  (# = $log_2{(C/K/N)}$)

  • Fully associative (1 set): 0 Index bits!
  • Direct-mapped (N = 1): max Index bits
  • N-way set-associative: somewhere in-between

• Tag: f identifying which memory block is currently in each cache slot (T = A – I – O)

type	Fields
Fully Associative	Tag		Offset
Direct-mapped	Tag	Index	Offset
N-way set-associative	Tag	Index	Offset

Fully Associative Cache

• Total bits

  In a slot:

  • Tag field of address as identifier (Tag bits)

  • Valid bit (1 bit): Whether cache slot was filled in

  • Dirty bit (1 bit if write-back)

  • Any necessary replacement management bits (“LRU bits”)

    Total bits in cache = $(C/K) \times (8 \times 2^{O} + Tag + 1 + 1 + ?)$ bits

• To check a fully associative cache

  1. Look at ALL cache slots in sequence
  2. If Valid bit is 0, then ignore
  3. If Valid bit is 1 and Tag matches, then return that data

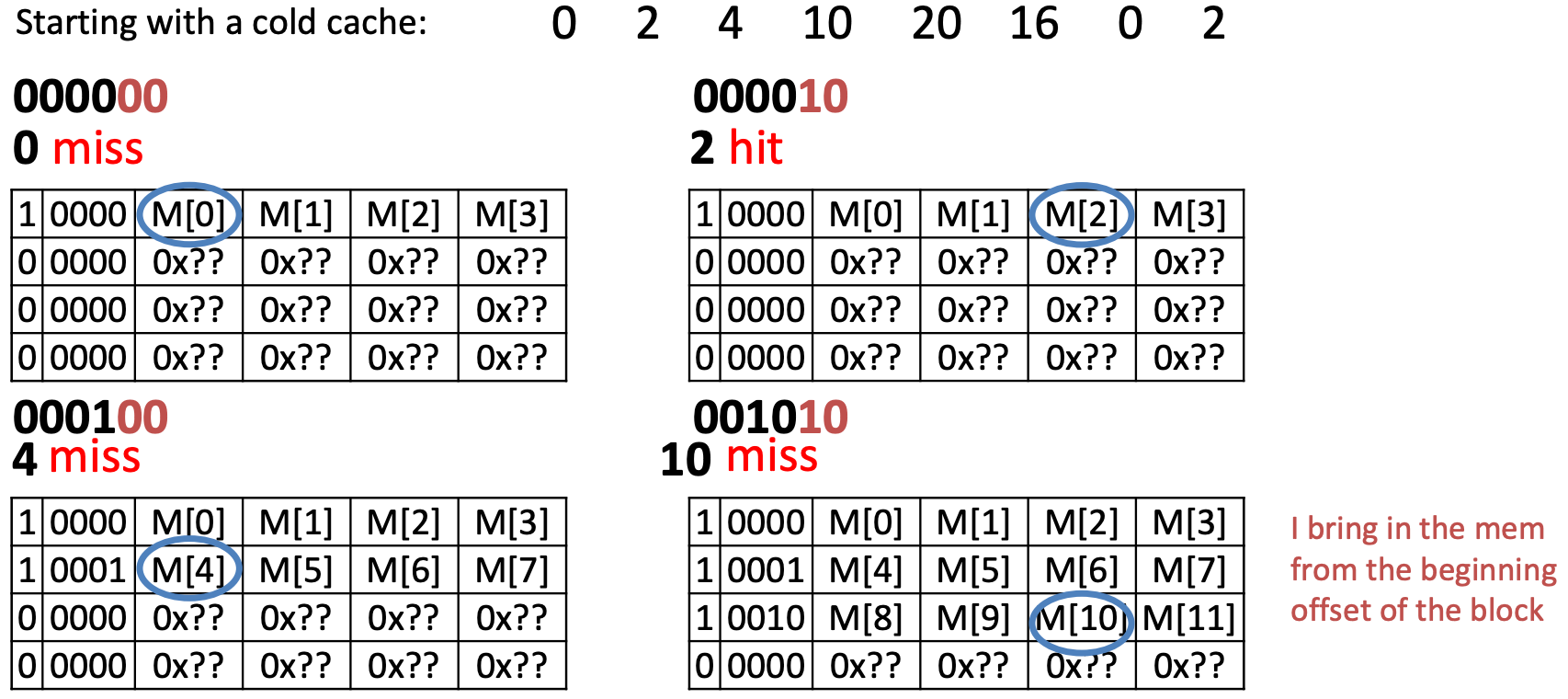
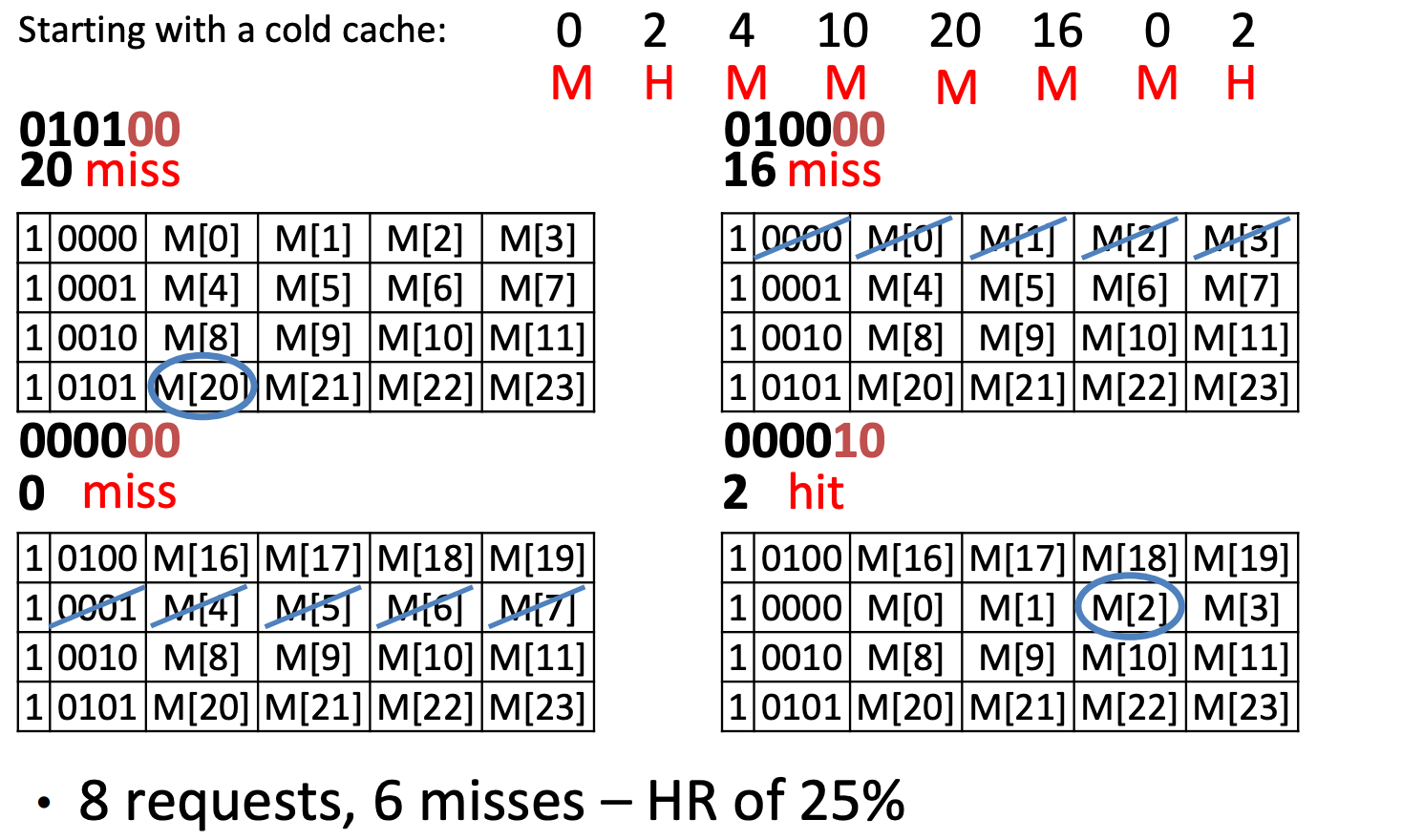
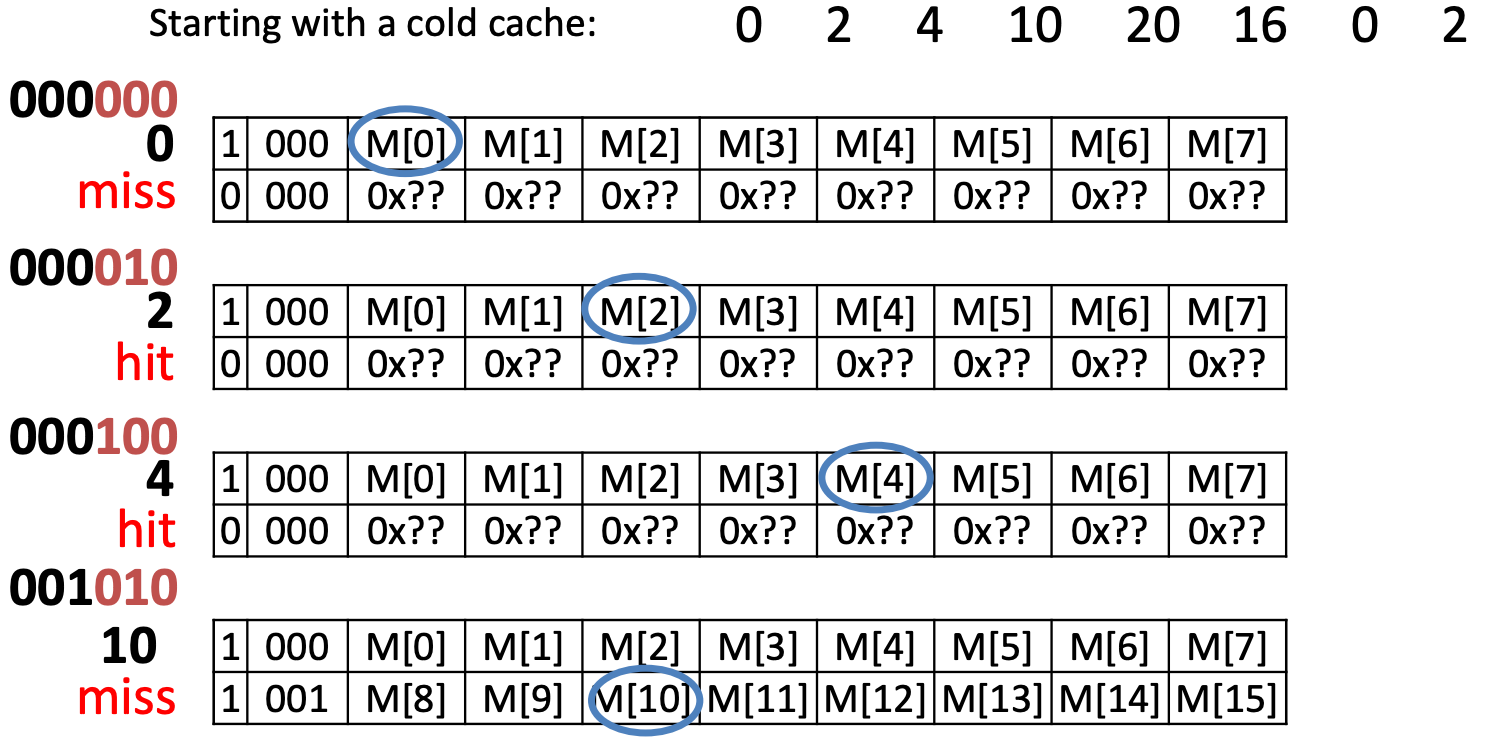
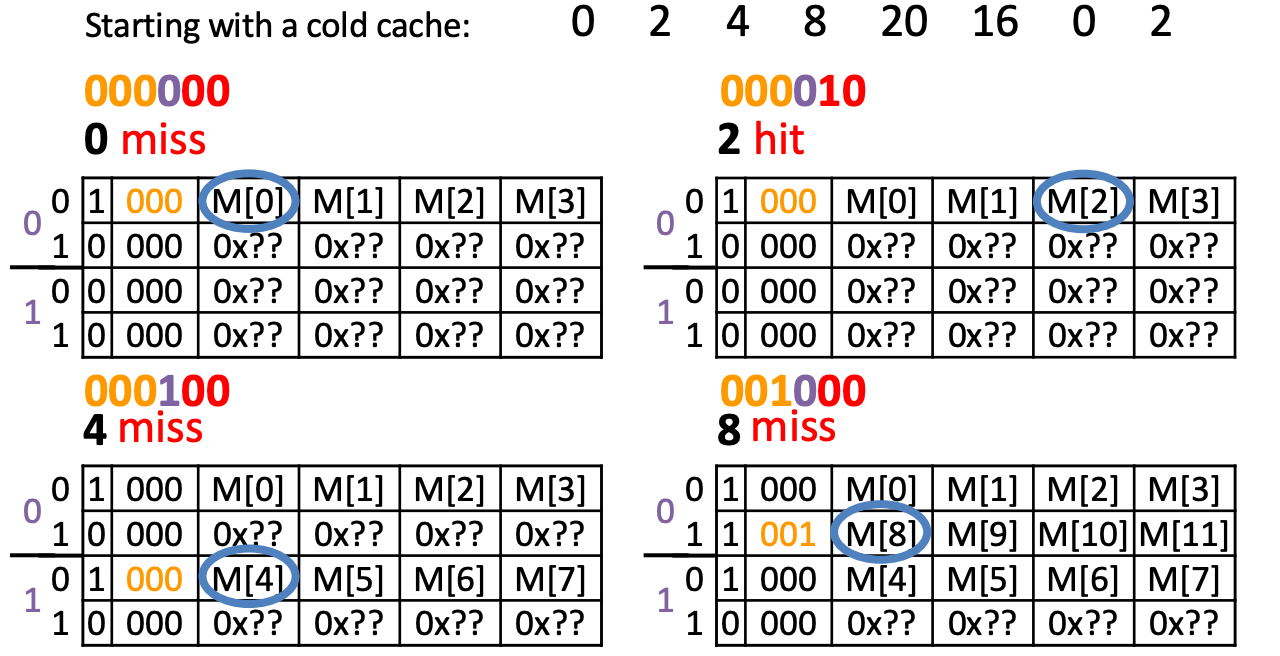
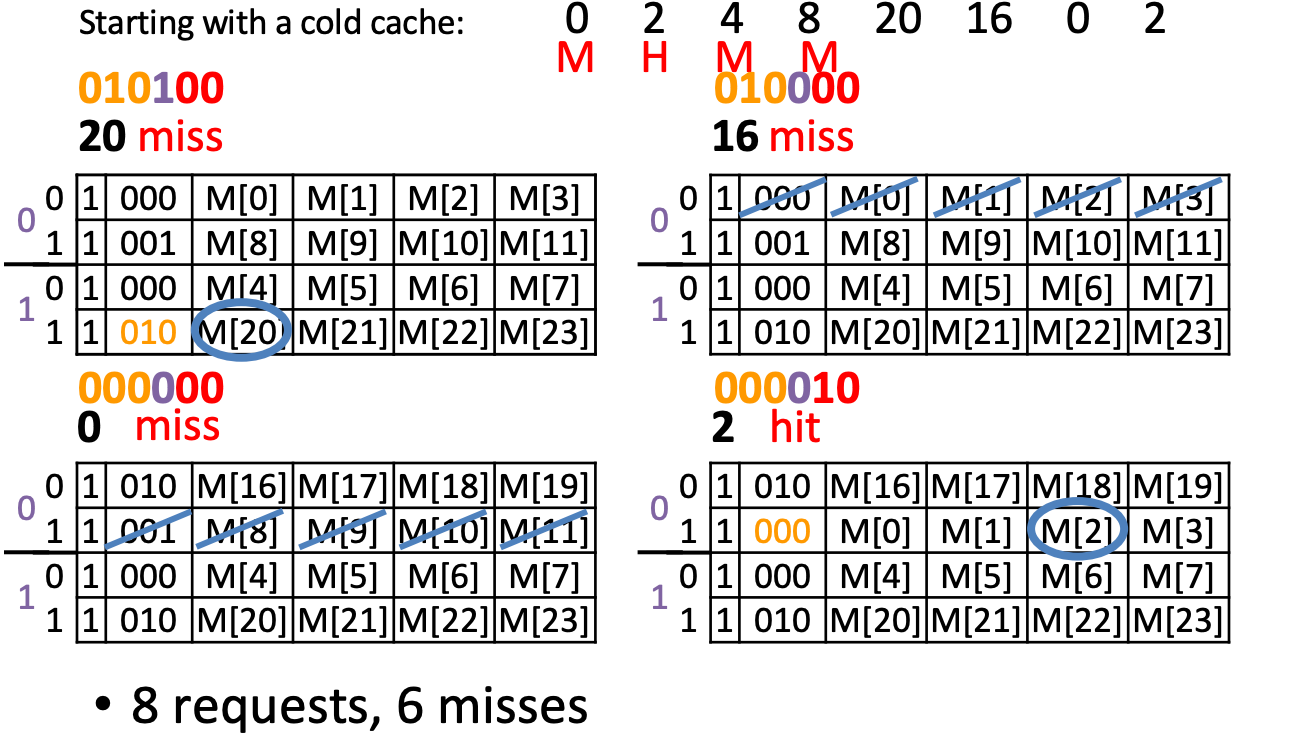
• Example

  Offset – 2 bits, Tag – 4 bits

  

  

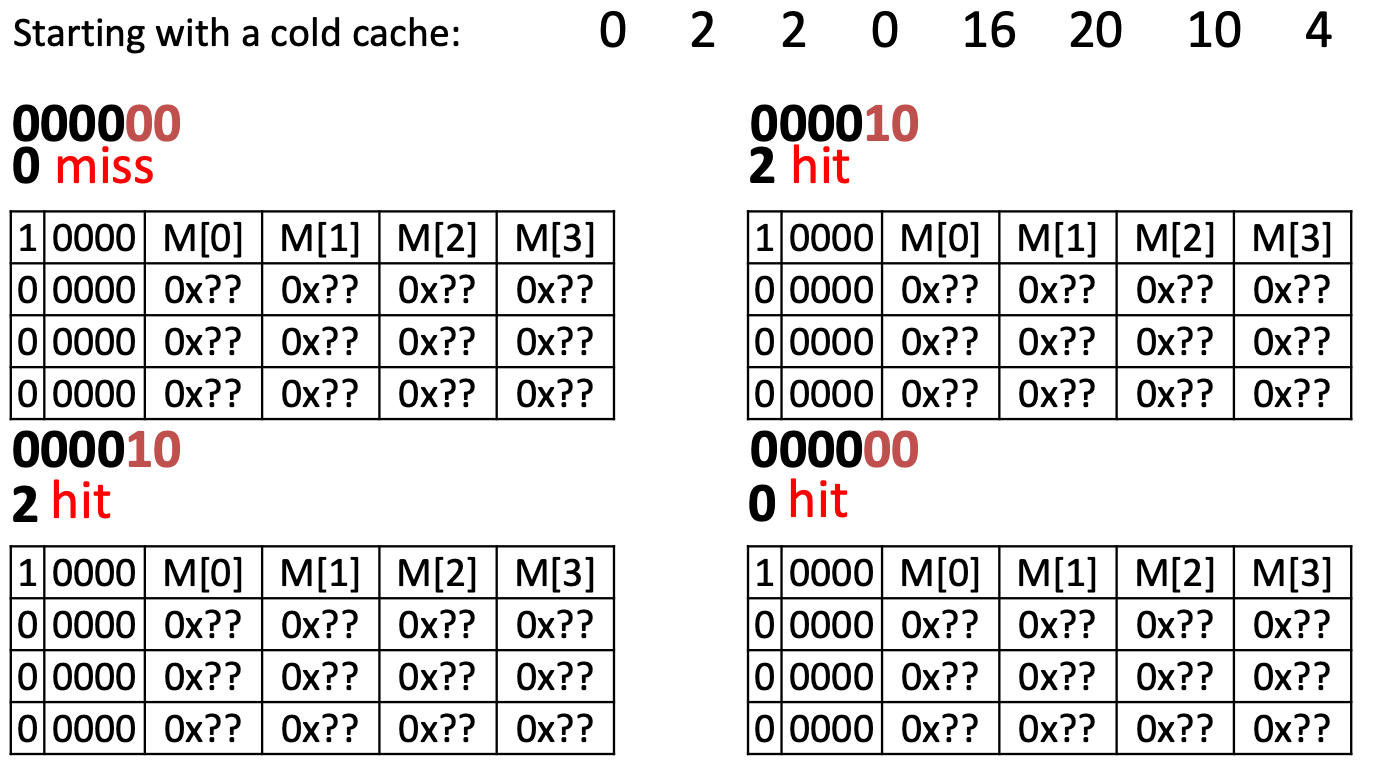
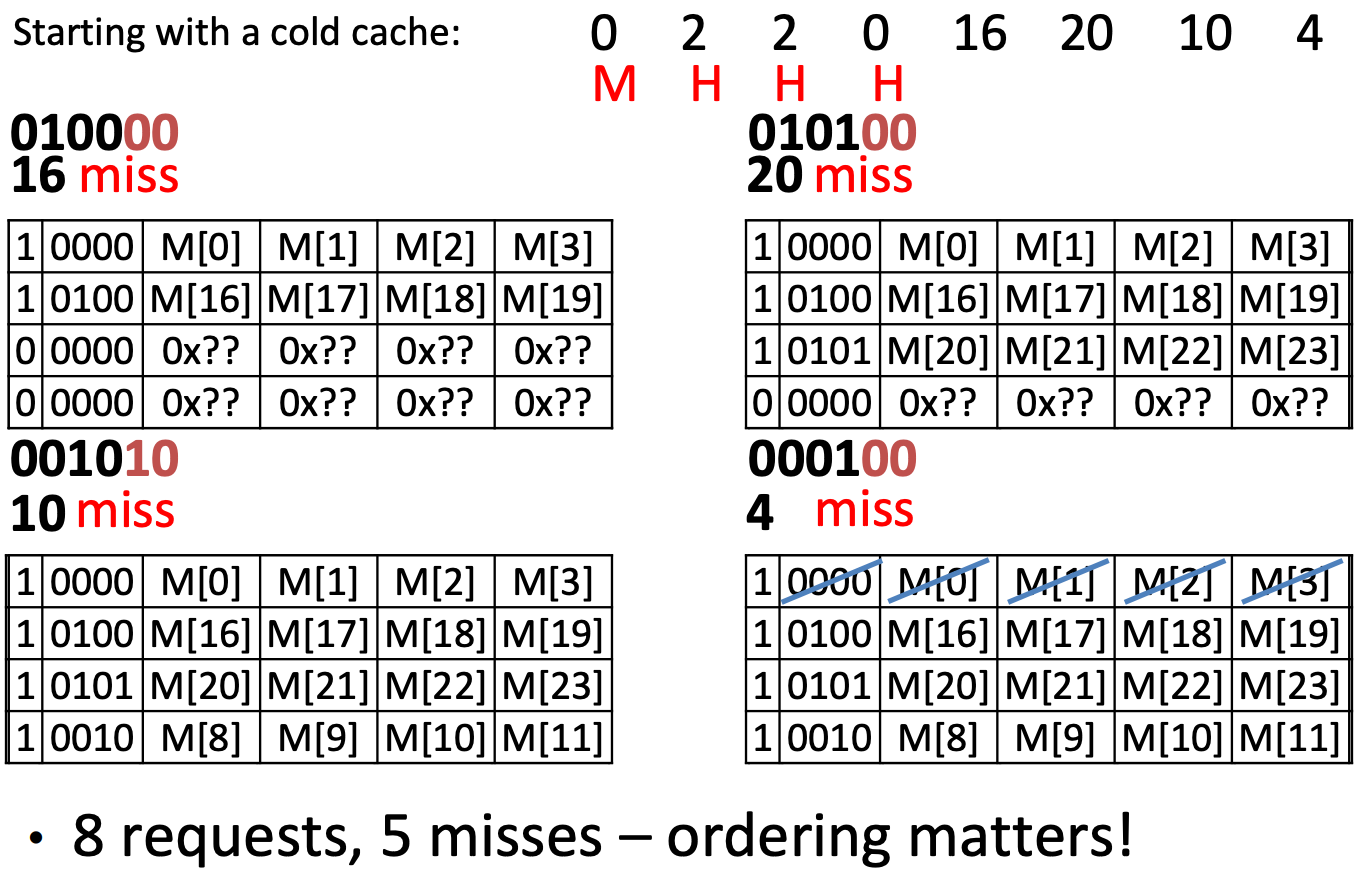
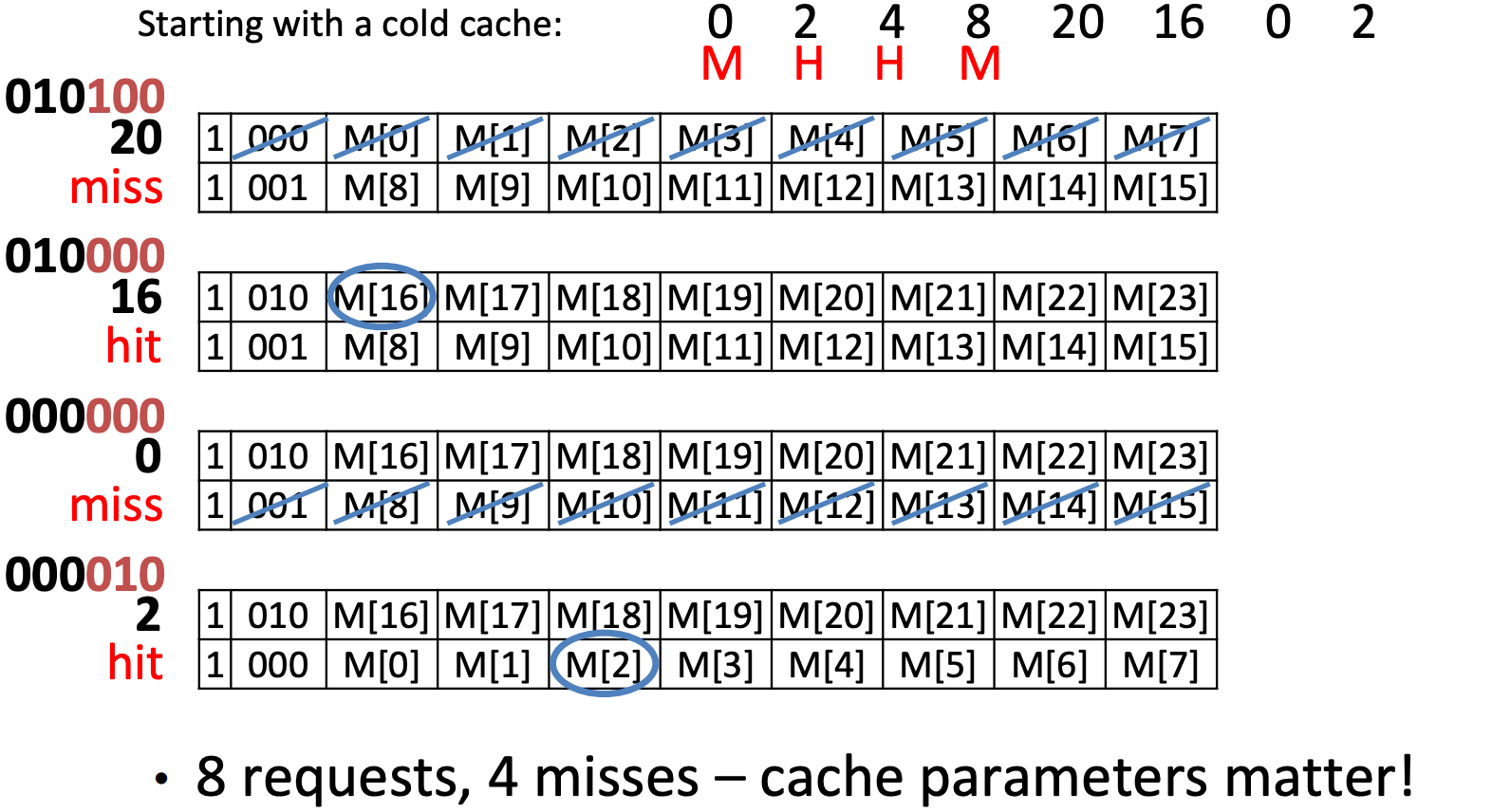
  Same requests, but reordered

  

  

  Original sequence, but double block size

  

  

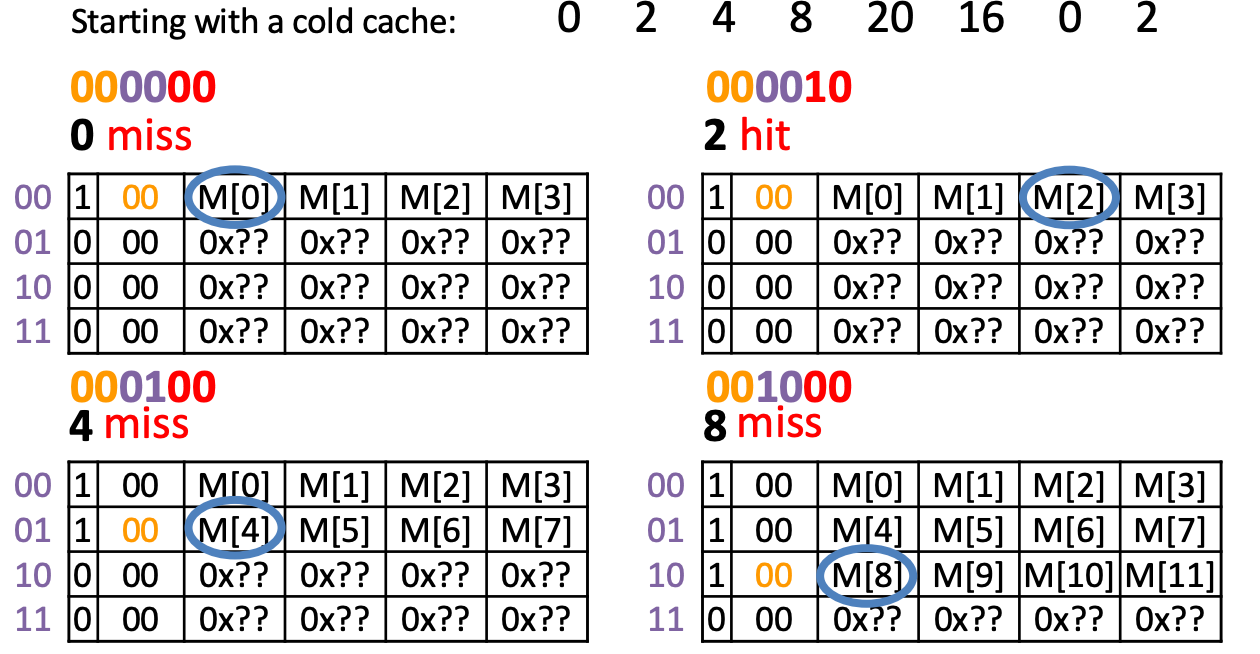
Direct-Mapped

• Total bits

  Total bits in cache = $(C/K) \times (8 \times 2^{O} + Tag + 1 + 1 + ?)$ bits

• Example

  

  

  

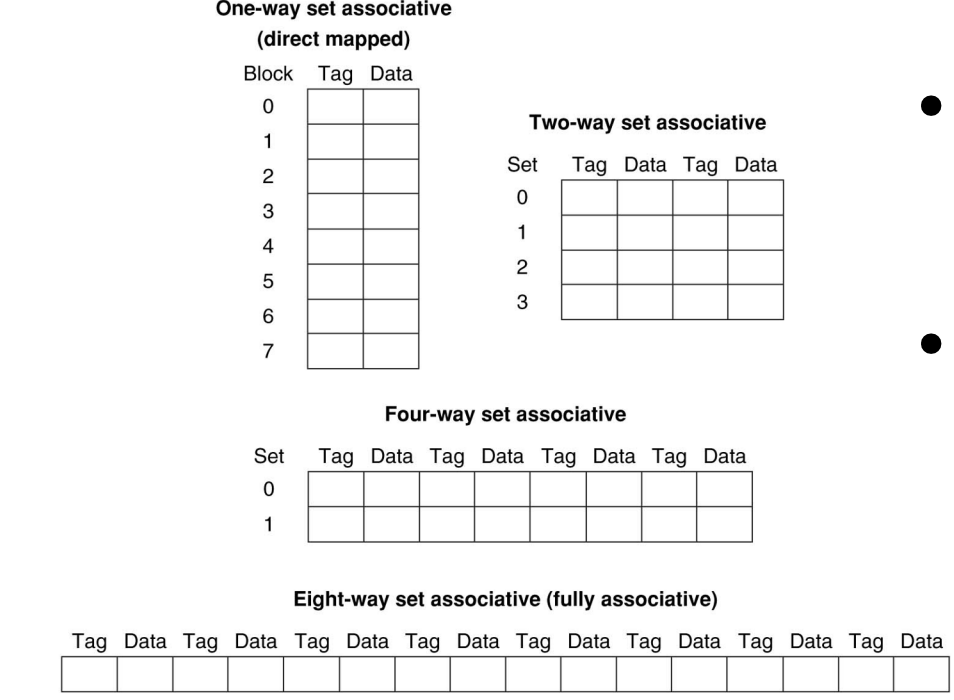
N-way set-associative

Divide Cache into sets, each of which consists of N slots

• Memory block maps to a set determined by Index field and is placed in any of the N slots of that set
• Replacement policy applies to every set

Total bits = $2^I \times N \times (8 \times 2^{O} + Tag + 1 + 1 + ?)$ bits

Example

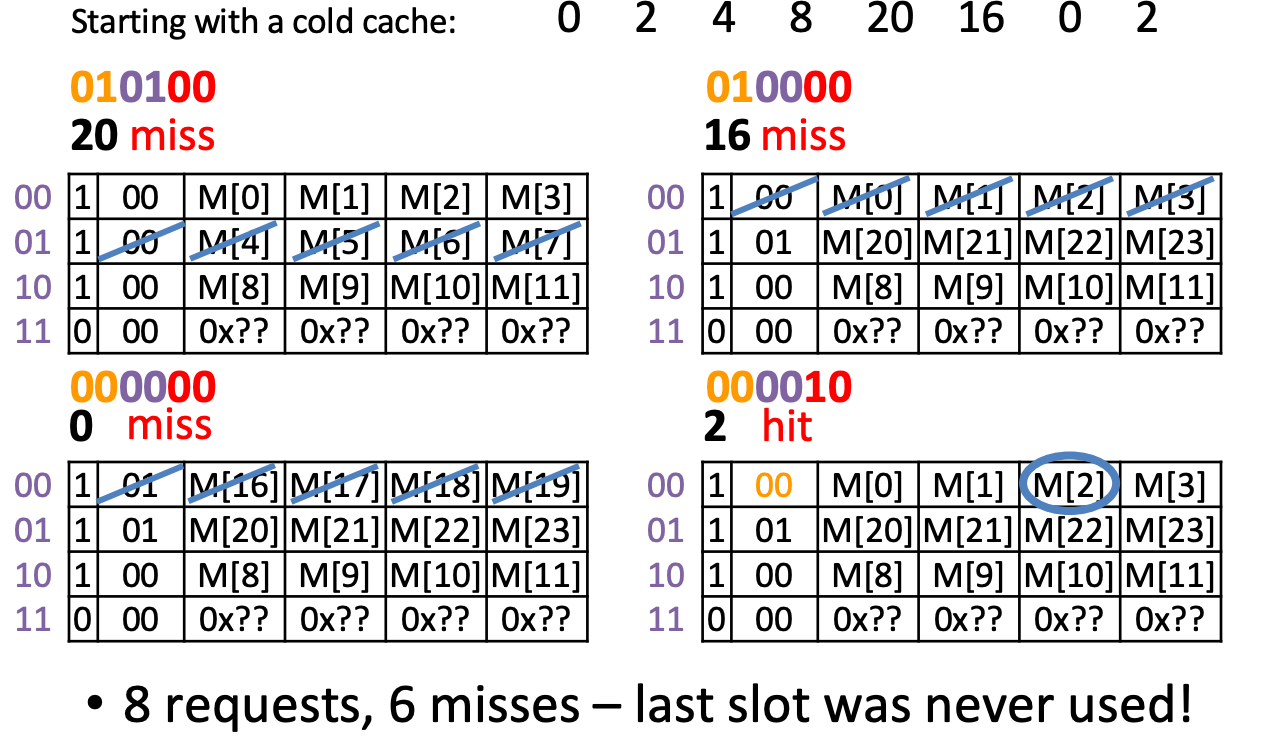
Compulsory Miss: 0(first),4,8,20,16

Capacity Miss: 0(second) (after its last access we have unique block accesses to 0001,0010,0101,0100, but we only have space for 4−1=3 more unique accesses)

Cache Questions

AMAT

3 parameters: Hit time, miss rate, miss penalty

• Hit Time
  • Cache size decreases → hit time decreases
  • associativity increases → hit time increases
• Miss Rate
  • Larger blocks, larger caches, more associativity can hold more data → miss rate decreases
  • Compiler optimizations
• Miss penalty
  • Multilevel caches
  • Smaller block size → lower MP

3Cs(Sources of Cache Misses):

• Compulsory: First access to block impossible to avoid
  • Increase block size (increases MP; too large blocks could increase MR because the number of blocks that can be held in the same size cache is smaller)
• Capacity: Cache cannot contain all blocks accessed by the program
  • Increase cache size (may increase HT)
• Conflict: Multiple memory locations mapped to the same cache location
  • Increase associativity (to fully associative) (may increase HT)
  • Increase block size(a set can hold more data)

Capacity or Conflict Miss

after the last access unique block accesses vs Fully Associative Space -1

Multilevel Caches

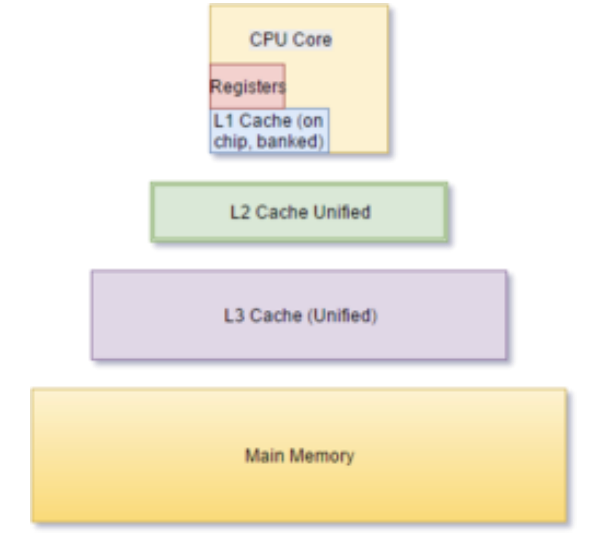
Design Considerations

• L1 cache focuses on low hit time (fast access)
  • e.g. smaller cache
• L2 L3 focus on low miss rate
  • e.g. larger cache with larger block sizes

Local vs. Global Miss Rates

• Local miss rate: Fraction of references to one level of a cache that miss
  • e.g. L2 local MR = L2 misses/L1 misses
• Global miss rate: Fraction of all references that miss in all levels of a multilevel cache
  • Global MR is the product of all local MRs

Compiler Optimization

Loop Interchange

By switching the order in which loops execute, misses can be reduced due to improvements in spatial locality.

/* Before */
for (k = 0; k < 100; k = k+1)
    for (j = 0; j < 100; j = j+1)
        for (i = 0; i < 5000; i = i+1)
            x[i][j] = 2 * x[i][j];
/* After */
for (k = 0; k < 100; k = k+1)
    for (i = 0; i < 5000; i = i+1)
        for (j = 0; j < 100; j = j+1)
            x[i][j] = 2 * x[i][j];

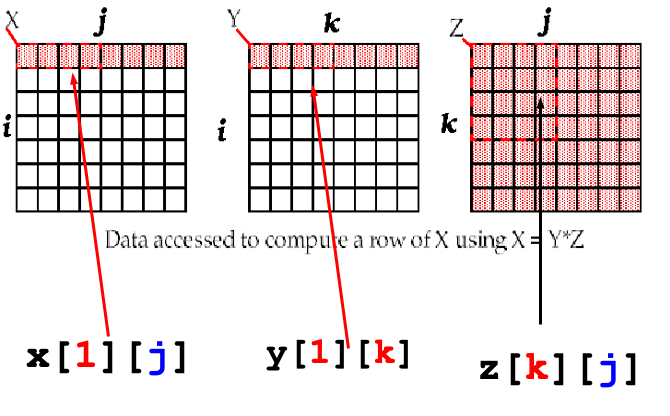
Matrix Multiply

Before capacity miss: $((N+N)N+N)\times N= 2N^3 + N^2$

After capacity miss: $(BN+BN)+B^2)\times(N/B)^2=2N^3/B + N^2$

/* Before */
for (i = 0; i < N; i = i+1)
    for (j = 0; j < N; j = j+1){
        r = 0;
        for (k = 0; k < N; k = k+1)
            r = r + y[i][k]*z[k][j];
        x[i][j] = r;
    };
/* After */
for (jj = 0; jj < N; jj = jj+B)
for (kk = 0; kk < N; kk = kk+B)
for (i = 0; i < N; i = i+1)
    for (j = jj; j < min(jj+B-1,N); j = j+1){
        r = 0;
        for (k = kk; k < min(kk+B-1,N); k = k+1)
            r = r + y[i][k]*z[k][j];
        x[i][j] = x[i][j] + r;
    };

• Y benefits from spatial locality
• Z benefits from temporal locality

Prefetching

cache size: 8kB, block size: 16 Bytes, data cache strategy: direct-mapped, write-back, write-allocate

The elements of a and b are 8 bytes long(double precision floating-point arrays)

//a[3][100] b[101][3]
for( i=0; i <3; i = i +1) 
    for( j=0; j<100; j=j+1)
        a[i][j] = b[j][0] * b[j+1][0];
//A[i][j]:Among 3*100,the even value of j will miss,the odd values will hit, total 150 misses
//B[j][0]：
//    j=0        B[0][0]、B[1][0]       2
//    j=1        B[1][0]、B[2][0]       1
//      ...
//    total  2+99=101 misses

Prefetch

for (j=0; j<100; j=j+1){
        Prefetch(b[j+7][0]);        
        prefetch(a[0][j+7]);
        a[0][j]=b[j][0]*b [j+1][0];}; 
// a[0][1] a[0][2] a[0][4] a[0][6]:4 misses
// b:2+5= 7 misses
for (i=1; i<3; i=i+1)
for (j=0; j<100; j=j+1){
        prefetch(a[i][j+7]);
        a[i][j]=b[j][0]*b [j+1][0];};
//4 misses for a[1][j]
//4 misses for a[2][j]
//Total:  19 misses
//save 232 cache misses at the price of 400 prefetch instructions.