3 Index & Hashing

B+ Tree

Structure

Node[…, ($P_i,K_i$), …]

$P_1$	$K_1$	$P_2$	...	$P_{n-1}$	$K_{n-1}$	$P_n$

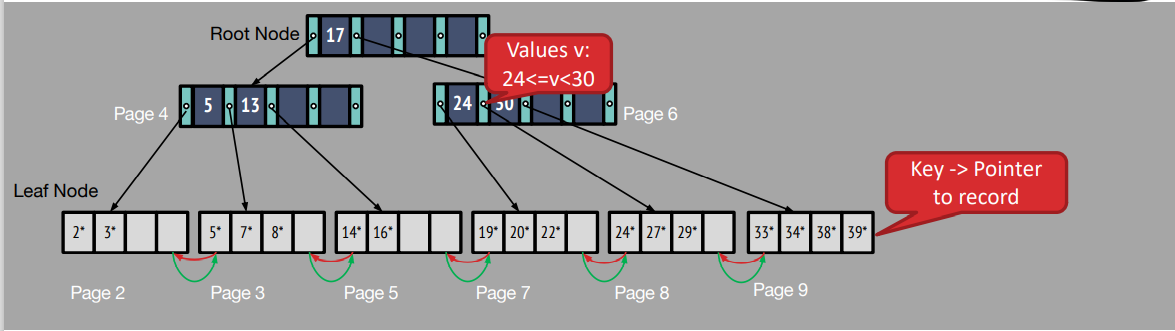
• Every root to leaf path has the same number of edges (the height of the tree). In this sense, B+ trees are always balanced.
• Only the leaf nodes contain records (or pointers to records). The inner nodes (which are the non-leaf nodes) do not contain the actual records.

Leaf Node

• For i = 1, 2, ..., n–1, pointer $P_i$ points to a file record with search-key value $K_i$

• $P_n$ points to next leaf node in search-key order

Non-Leaf Node

• All the search-keys in the subtree to which $P_i$ points have values greater than or equal to $K_{i-1}$ and less than $K_i$

• All the search-keys in the subtree to which $P_n$ points have values greater than or equal to $K_{n-1}$

Occupancy Invariant

• Each node that is not a root or a leaf has between$\lceil n/2 \rceil$ and n children.
• A leaf node has between $\lceil (n-1)/2 \rceil$ and n–1 values
• Special cases:
  • If the root is not a leaf, it has at least 2 children.
  • If the root is a leaf (that is, there are no other nodes in the tree), it can have between 0 and (n–1) values

Insertion

To insert an entry into the B+ tree, follow this procedure:

1. Find the leaf node L, insert (pointer,key-value) pair in the leaf node

2. If L overflows

• LeafNode: 看 Key

  • (1)take the 2d+1 (pointer,search-key value) pairs (including the one being inserted,also there is a next pointer) in sorted order. Split into L1 and L2. Keep d pairs in L1 (this means d + 1 pairs will go in L2).
  • (2)If L was a leaf node, COPY L2’s first pair into the parent. If L was not a leaf node, MOVE L2’s first pair into the parent.

• NonLeafNode: 看pointers(Childrens)

  • (1) Split n+1 pointers into L1 and L2. Keep $\lfloor{(n+1)/2}\rfloor$ in L1, rest go to L2.
  • (2) MOVE L2’s first pair(pointer这里只移动线,不带对象) into the parent.
  • (3) reorder leaves

3. If the parent overflows, then recurse on it by doing step 2 on the parent.

Why copy/move?

• we want to COPY leaf node data into the parent so that we don’t lose the data in the leaf node. Remember that every key that is in the table that the index is built on must be in the leaf nodes! Being in a inner node does not mean that key is actually still in the table.
• we can MOVE inner node data into parent nodes because the inner node does not contain the actual data, they are just a reference of which way to search when traversing the tree.